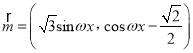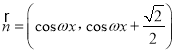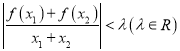题目内容
【题目】已知函数![]() .
.
(1)求证:当![]() 时,函数
时,函数![]() 在
在![]() 上,存在唯一的零点;
上,存在唯一的零点;
(2)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)(0,1).
【解析】试题分析:(1)先证明函数![]() 在(0,+∞)上单调递增,再根据零点存在定理证明
在(0,+∞)上单调递增,再根据零点存在定理证明![]() 上存在零点即可。(2)“若存在
上存在零点即可。(2)“若存在![]() ,使得
,使得![]() 成立”转化为
成立”转化为
“![]() ”,利用导数可得
”,利用导数可得![]()
![]() ,从而由
,从而由![]() 得
得![]() ,设g(a)=lna+a﹣1,由g(a)的单调性可得当0<a<1时,g(a)<0,故所求范围为(0,1)。
,设g(a)=lna+a﹣1,由g(a)的单调性可得当0<a<1时,g(a)<0,故所求范围为(0,1)。
试题解析:
(1)证明:∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴函数f(x)在(0,+∞)上单调递增,
又当a≤0时, ![]() ,
, ![]() ,
,
所以函数![]() 上存在唯一零点。
上存在唯一零点。
(2)由(1)得![]() ,
,
∵a>0,
∴当x∈(0, ![]() )时,f′(x)>0,f(x)单调递增;
)时,f′(x)>0,f(x)单调递增;
当x∈(![]() ,+∞)时,f′(x)<0,f(x)单调递减。
,+∞)时,f′(x)<0,f(x)单调递减。
∴![]() 在x=
在x=![]() 时取得最大值,且最大值为
时取得最大值,且最大值为![]() 。
。
“存在![]() ”等价于
”等价于![]()
![]()
∴![]() ,
,
∴![]() ,
,
令g(a)=lna+a﹣1
∵g(a)在(0,+∞)单调递增,且g(1)=0,
∴当0<a<1时,g(a)<0;当a>1时,g(a)>0。
∴a的取值范围为(0,1)。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】(某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示: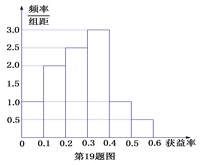
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验若每份保单的保费在 ![]() 元的基础上每增加
元的基础上每增加 ![]() 元,对应的销量
元,对应的销量 ![]() (万份)与
(万份)与 ![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下
(元)有较强线性相关关系,从历史销售记录中抽样得到如下 ![]() 组
组 ![]() 与
与 ![]() 的对应数据:
的对应数据:
|
|
|
|
|
|
销量 |
|
|
|
|
|
(ⅰ)根据数据计算出销量 ![]() (万份)与
(万份)与 ![]() (元)的回归方程为
(元)的回归方程为 ![]() ;
;
(ⅱ)若把回归方程 ![]() 当作
当作 ![]() 与
与 ![]() 的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
参考公示: