题目内容
已知点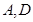 分别是椭圆
分别是椭圆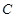 :
: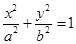 (
(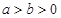 )的左顶点和上顶点,椭圆的左右焦点分别是
)的左顶点和上顶点,椭圆的左右焦点分别是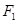 和
和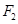 ,点
,点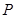 是线段
是线段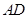 上的动点,如果
上的动点,如果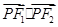 的最大值是
的最大值是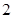 ,最小值是
,最小值是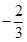 ,那么,椭圆的
,那么,椭圆的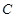 的标准方程是 .
的标准方程是 .
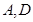 分别是椭圆
分别是椭圆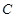 :
: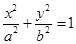 (
(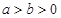 )的左顶点和上顶点,椭圆的左右焦点分别是
)的左顶点和上顶点,椭圆的左右焦点分别是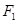 和
和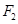 ,点
,点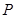 是线段
是线段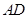 上的动点,如果
上的动点,如果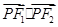 的最大值是
的最大值是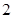 ,最小值是
,最小值是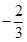 ,那么,椭圆的
,那么,椭圆的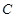 的标准方程是 .
的标准方程是 . 
试题分析:当
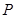 在A点时
在A点时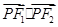 最大,此时
最大,此时 ,设直线AD与圆交于M,N两点,P在MN中点时
,设直线AD与圆交于M,N两点,P在MN中点时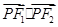 最小,设中点为C
最小,设中点为C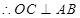 ,
, 直线为
直线为
 直线为
直线为 ,联立方程的
,联立方程的
 最小值为
最小值为
 ,椭圆的
,椭圆的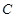 的标准方程
的标准方程
点评:本题关键是找到取得最大值最小值的点的位置

练习册系列答案
相关题目
 :
:
 过点
过点 ,上、下焦点分别为
,上、下焦点分别为 、
、 ,
, .直线
.直线 与椭圆交于
与椭圆交于 两点,线段
两点,线段 中点为
中点为 .
. ,若曲线
,若曲线 与区域
与区域 的最小值.
的最小值. 过点
过点 ,且离心率
,且离心率 .
. 的标准方程;
的标准方程; 的直线
的直线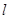 交椭圆于不同的两点M、N,且满足
交椭圆于不同的两点M、N,且满足 (其中点O为坐标原点),若存在,求出直线
(其中点O为坐标原点),若存在,求出直线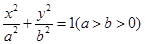 ,
,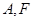 是其左顶点和左焦点,
是其左顶点和左焦点,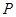 是圆
是圆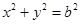 上的动点,若
上的动点,若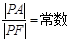 ,则此椭圆的离心率是
,则此椭圆的离心率是 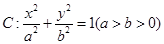 ,
,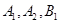 是椭圆
是椭圆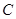 的顶点,若椭圆
的顶点,若椭圆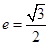 ,且过点
,且过点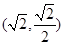 .
.
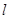 ,使得
,使得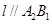 ,且与椭圆
,且与椭圆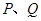 两点(异于椭圆
两点(异于椭圆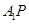 和直线
和直线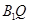 的倾斜角分别是
的倾斜角分别是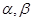 ,求证:
,求证: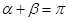 .
.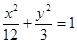 的左焦点为
的左焦点为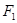 , 点
, 点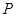 在椭圆上, 如果线段
在椭圆上, 如果线段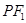 的中点
的中点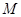 在
在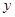 轴的
轴的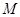 的坐标是 .
的坐标是 .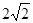 ,0)和F2(
,0)和F2(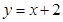 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。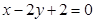 经过椭圆
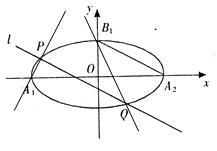
经过椭圆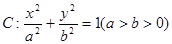 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆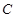 的右顶点为
的右顶点为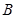 ,点
,点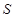 是椭圆
是椭圆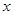 轴上方的动点,直线
轴上方的动点,直线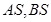 与直线
与直线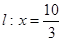 分别交于
分别交于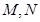 两点。
两点。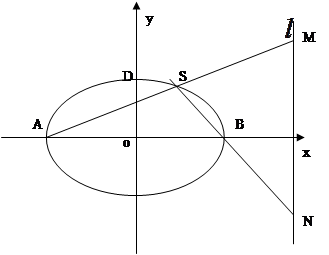
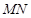 的长度的最小值;
的长度的最小值;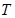 ,使得
,使得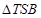 的面积为
的面积为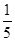 ?若存在,确定点
?若存在,确定点