题目内容
椭圆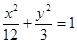 的左焦点为
的左焦点为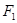 , 点
, 点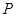 在椭圆上, 如果线段
在椭圆上, 如果线段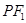 的中点
的中点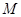 在
在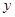 轴的
轴的
正半轴上, 那么点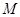 的坐标是 .
的坐标是 .
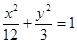 的左焦点为
的左焦点为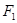 , 点
, 点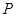 在椭圆上, 如果线段
在椭圆上, 如果线段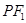 的中点
的中点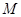 在
在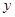 轴的
轴的正半轴上, 那么点
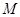 的坐标是 .
的坐标是 .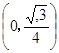
试题分析:因为线段PF1的中点M在y轴的正半轴上,所以MO是△PF1F2的中位线,因为MO⊥x轴,所以PF2⊥x轴,所以|PF2| =
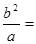
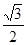 。所以P点坐标为
。所以P点坐标为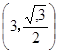 ,所以M点坐标为
,所以M点坐标为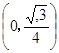 。
。点评:本题考查椭圆的简单性质和应用,解题时要认真审题,注意三角形中位线的合理应用.属于基础题型。

练习册系列答案
相关题目
 :
: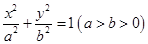 的离心率为
的离心率为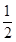 ,
,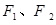 分别为椭圆
分别为椭圆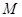 为椭圆上任意一点,以
为椭圆上任意一点,以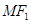 为半径作圆
为半径作圆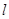 有公共点时,求△
有公共点时,求△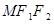 面积的最大值.
面积的最大值.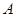 是椭圆
是椭圆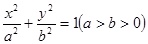 上一点,
上一点,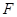 为椭圆的一个焦点,且
为椭圆的一个焦点,且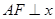 轴,
轴,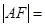 焦距,则椭圆的离心率是( )
焦距,则椭圆的离心率是( ) 
 -1
-1 -1
-1
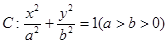 过点
过点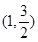 ,且离心率e=
,且离心率e=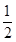 .
.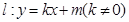 与椭圆交于不同的两点
与椭圆交于不同的两点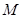 、
、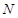 ,且线段
,且线段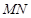 的垂直平分线过定点
的垂直平分线过定点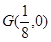 ,求
,求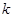 的取值范围。
的取值范围。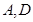 分别是椭圆
分别是椭圆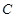 :
: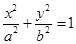 (
(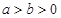 )的左顶点和上顶点,椭圆的左右焦点分别是
)的左顶点和上顶点,椭圆的左右焦点分别是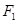 和
和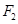 ,点
,点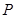 是线段
是线段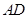 上的动点,如果
上的动点,如果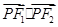 的最大值是
的最大值是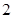 ,最小值是
,最小值是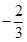 ,那么,椭圆的
,那么,椭圆的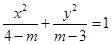 表示焦点在
表示焦点在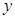 轴上的椭圆,则
轴上的椭圆,则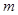 的取值范围是 ( )
的取值范围是 ( )



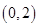 ,且离心率为
,且离心率为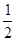 的椭圆的标准方程是________________。
的椭圆的标准方程是________________。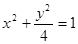 的离心率为( )
的离心率为( )


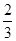
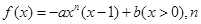 为正整数,
为正整数,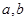 为常数.曲线
为常数.曲线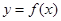 在点
在点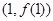 处的切线方程为
处的切线方程为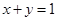 .
.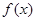 的最大值;
的最大值;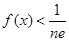 .
.