题目内容
8.已知三棱柱ABC-A1B1C1中,D是AC的中点,求证:AB1∥平面DBC1.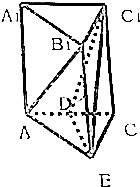
分析 取A1C1的中点E,由已知条件推导出面AB1E∥面BDC1,由此能证明AB1∥面DBC1.
解答 证明:取A1C1的中点E,连结DE,AE,B1E,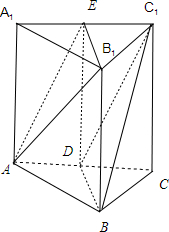
∵三棱柱ABC-A1B1C1中,D是AC的中点,
∴BB1$\underset{∥}{=}$DE,AD$\underset{∥}{=}$EC1,
∴四边形BB1ED是平行四边形,四边形AEC1D是平行四边形,
∴BD∥B1E,AE∥DC1,又∵AE∩B1E=E,BD∩C1D=D,
∴面AB1E∥面BDC1,
又∵AB1?面AB1E,∴AB1∥面DBC1.
点评 本题考查线面平行的证明,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
18.${∫}_{-1}^{1}$(sinx+x2)dx=( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
20.已知随机变量X服从正态分布N(2,σ2),P(X≤3)=0.72,则P(1<X<3)等于( )
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
17.若sinα=-$\frac{3}{5}$,α是第三象限的角,则$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
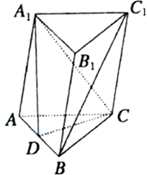 如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.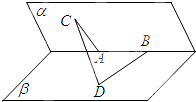 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.