题目内容
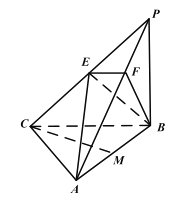
【题目】在三棱锥![]() 中,
中, ![]() 底面
底面![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)由PB⊥底面ABC,可证AC⊥PB,由∠BCA=90°,可得AC⊥CB.又PB∩CB=B,即可证明AC⊥平面PBC.
(2)取AF的中点G,连结CG,GM.可得EF∥CG.又CG平面BEF,有EF平面BEF,有CG∥平面BEF,同理证明GM∥平面BEF,有平面CMG∥平面BEF,即可证明CM∥平面BEF.
(3)取BC中点D,连结ED,可得ED∥PB,由PB⊥底面ABC,故ED⊥底面ABC,由PB=BC=CA=2,即可求得三棱锥E-ABC的体积.
试题解析:
(1)因为![]() 底面
底面![]() ,且
,且![]() 底面
底面![]() ,
,
所以![]() .
.
由![]() ,可得
,可得![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 中点.
中点.
在![]() 中,
中, ![]() 分别为
分别为![]() 中点.
中点.
所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
同理可证![]() 平面
平面![]() .
.
又![]() ,
,
所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)取![]() 中点
中点![]() ,连接
,连接![]() .
.
在![]() 中,
中, ![]() 分别为中点,所以
分别为中点,所以![]() ,
,
因为![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() .
.
由![]() ,可得
,可得![]() .
.


练习册系列答案
相关题目


