题目内容
9.非零向量$\overrightarrow a,\overrightarrow b$夹角为60°,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为( )| A. | (1,$\sqrt{3}$] | B. | (0,$\sqrt{3}$] | C. | (1,2] | D. | [1,2] |
分析 对$|\overrightarrow{a}-\overrightarrow{b}|=1$两边平方,便得${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=1$,从而$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=1+4\overrightarrow{a}•\overrightarrow{b}$=$1+2|\overrightarrow{a}||\overrightarrow{b}|$,这样只要求$|\overrightarrow{a}||\overrightarrow{b}|$的范围即可:根据$|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}=1+|\overrightarrow{a}||\overrightarrow{b}|$便可得出$1+|\overrightarrow{a}||\overrightarrow{b}|≥2|\overrightarrow{a}||\overrightarrow{b}|$,这样便可得出$|\overrightarrow{a}||\overrightarrow{b}|$的范围,从而得出$|\overrightarrow{a}+\overrightarrow{b}|$的取值范围.
解答 解:$|\overrightarrow{a}-\overrightarrow{b}|=1$;
∴${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=1$,$\overrightarrow{a}$,$\overrightarrow{b}$夹角为60°;
∴$|\overrightarrow{a}{|}^{2}-|\overrightarrow{a}||\overrightarrow{b}|+|\overrightarrow{b}{|}^{2}=1$;
∴$|\overrightarrow{a}||\overrightarrow{b}|+1=|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}≥2|\overrightarrow{a}||\overrightarrow{b}|$;
$0<|\overrightarrow{a}||\overrightarrow{b}|≤1$;
∴$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}+4\overrightarrow{a}•\overrightarrow{b}=1+4\overrightarrow{a}•\overrightarrow{b}=1+2|\overrightarrow{a}||\overrightarrow{b}|$;
∴$1<|\overrightarrow{a}+\overrightarrow{b}{|}^{2}≤3$;
∴$1<|\overrightarrow{a}+\overrightarrow{b}|≤\sqrt{3}$;
∴$|\overrightarrow{a}+\overrightarrow{b}|$的取值范围为$(1,\sqrt{3}]$.
故选A.
点评 考查向量长度$|\overrightarrow{a}|=\sqrt{{\overrightarrow{a}}^{2}}$,向量数量积的运算及其计算公式,基本不等式在求范围中的应用,完全平方式的运用.

 阅读快车系列答案
阅读快车系列答案| A. | 在△ABC中,A<B是sinA<sinB的充要条件 | |
| B. | $\overrightarrow{a}$$•\overrightarrow{b}$<0 是$\overrightarrow{a}$与$\overrightarrow{b}$夹角为钝角的充要条件 | |
| C. | 若直线a,b,平面α,β满足a⊥α,α⊥β,b?α,b?β则a⊥b能推出b⊥β | |
| D. | 在相关性检验中,当相关性系数r满足|r|>0.632时,才能求回归直线方程 |
| A. | λ=-$\frac{1}{2}$ | B. | λ=-2或-$\frac{1}{2}$ | C. | λ≠-2 | D. | λ≠1且λ≠-2 |
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
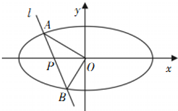 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.