题目内容
4.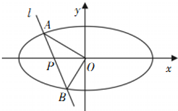 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.(Ⅰ)求椭圆C的方程;
(Ⅱ) 求△AOB面积的最大值.
分析 (Ⅰ)通过短轴的一个端点到右焦点的距离为2可知a=2,进而利用离心率的值计算即得结论;
(Ⅱ)设直线l的方程为x=my-1,代入椭圆方程,整理,利用韦达定理,计算三角形的面积,换元,利用函数的单调性,即可求得结论.
解答 解:(Ⅰ)由题意可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{a=2}\end{array}\right.$,
解得:a=2,c=$\sqrt{3}$,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(Ⅱ)设直线l的方程为x=my-1,代入椭圆方程,整理可得
(m2+4)y2-2my-3=0,
设A(x1,y1),B(x2,y2),
y1y2=$\frac{-3}{{m}^{2}+4}$,y1+y2=$\frac{2m}{{m}^{2}+4}$,
∴|y1-y2|=$\frac{4\sqrt{{m}^{2}+3}}{{m}^{2}+4}$,
∴△AOB的面积S=$\frac{1}{2}$|OP||y1-y2|=$\frac{2}{\sqrt{{m}^{2}+3}+\frac{1}{\sqrt{{m}^{2}+3}}}$
设t=$\sqrt{{m}^{2}+3}$(t≥$\sqrt{3}$),则g(t)=t+$\frac{1}{t}$在[$\sqrt{3}$,+∞)上为增函数,
∴g(t)≥$\frac{4\sqrt{3}}{3}$,
∴S≤$\frac{\sqrt{3}}{2}$,当且仅当m=0时,△AOB的面积最大值为$\frac{\sqrt{3}}{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查三角形面积的计算,考查运算求解能力,属于中档题.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | (1,$\sqrt{3}$] | B. | (0,$\sqrt{3}$] | C. | (1,2] | D. | [1,2] |
| A. | [0,$\frac{1}{2}$) | B. | [0,$\frac{1}{4}$) | C. | [0,$\frac{1}{8}$) | D. | [0,$\frac{1}{16}$) |
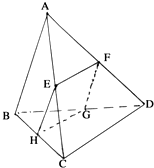 如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.
如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形. 如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.
如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.