题目内容
如图,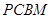 是直角梯形,∠
是直角梯形,∠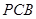 =90°,
=90°,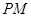 ∥
∥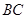 ,
,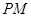 =1,
=1,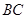 =2,又
=2,又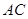 =1,∠
=1,∠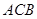 =120°,
=120°,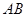 ⊥
⊥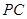 ,直线
,直线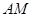 与直线
与直线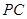 所成的角为60°.
所成的角为60°.
(1)求二面角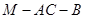 的的余弦值;
的的余弦值;
(2)求点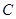 到面
到面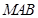 的距离.
的距离.
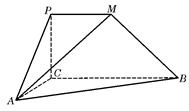
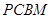 是直角梯形,∠
是直角梯形,∠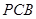 =90°,
=90°,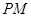 ∥
∥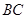 ,
,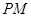 =1,
=1,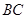 =2,又
=2,又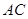 =1,∠
=1,∠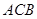 =120°,
=120°,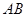 ⊥
⊥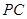 ,直线
,直线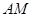 与直线
与直线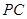 所成的角为60°.
所成的角为60°.(1)求二面角
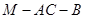 的的余弦值;
的的余弦值;(2)求点
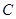 到面
到面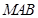 的距离.
的距离.
(1)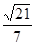 ;(2)
;(2)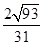 .
.
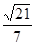 ;(2)
;(2)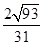 .
.试题分析:此题可用向量法来求解.(1)由题意易知
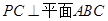 ,则在平面
,则在平面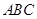 内过点
内过点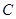 作
作 交
交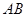 于点
于点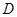 ,分别以
,分别以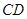 、
、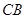 、
、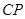 为
为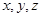 轴,
轴,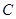 为原点建立空间直角坐标系
为原点建立空间直角坐标系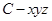 ,找出相应点的坐标,由直线
,找出相应点的坐标,由直线 与直线
与直线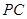 所成角为
所成角为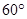 ,求出点
,求出点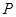 的坐标,从而可确定点
的坐标,从而可确定点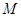 的坐标,由平面
的坐标,由平面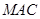 内向量
内向量 、
、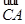 可求得平面平面
可求得平面平面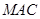 的法向量
的法向量 ,平面
,平面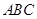 法向量为
法向量为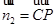 ,根据向量的数量积公式,可求出向量
,根据向量的数量积公式,可求出向量 与
与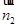 夹角的余弦值,从而求出所求二面角的余弦值;(2)先求出平面
夹角的余弦值,从而求出所求二面角的余弦值;(2)先求出平面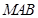 的法向量
的法向量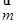 ,又点
,又点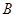 在平面
在平面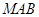 内,可求出向量
内,可求出向量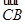 的坐标,由点到平面的向量计算公式
的坐标,由点到平面的向量计算公式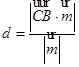 可求得点
可求得点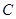 到平面
到平面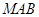 的距离.
的距离.试题解析:(1)∵
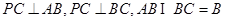 ∴
∴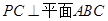 .
.在平面
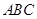 内,过
内,过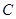 作
作 ,建立空间直角坐标系
,建立空间直角坐标系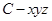 (如图)
(如图)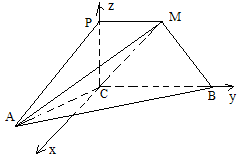
由题意有
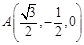 ,设
,设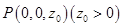 ,
,则
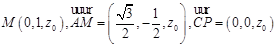
由直线
 与直线
与直线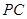 所成的解为
所成的解为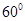 ,得
,得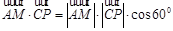 ,
,即
 ,解得
,解得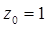
∴
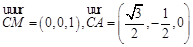 ,设平面
,设平面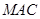 的一个法向量为
的一个法向量为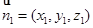 ,
,则
 ,取
,取 ,得
,得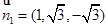 ,平面
,平面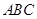 的法向量取为
的法向量取为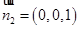
设
 与
与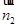 所成的角为
所成的角为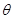 ,则
,则 .
.显然,二面角
 的平面角为锐角,故二面角
的平面角为锐角,故二面角 的余弦值为
的余弦值为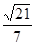 . 5分
. 5分(2)
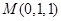 ,
,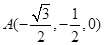 ,
,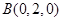 ,
,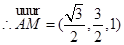 ,
,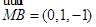 .
.设平面
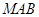 的一个法向量
的一个法向量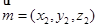 ,则
,则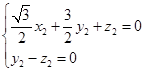 ,
,取
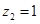 ,得
,得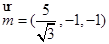 ,则点
,则点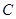 到平面
到平面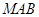 的距离
的距离 . 10分
. 10分
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
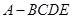 中,平面
中,平面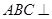 平面
平面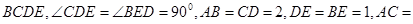
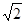 .
.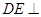 平面
平面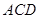 ;
;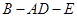 的大小
的大小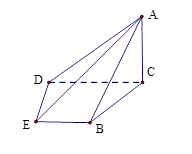
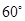 ,∠BAC
,∠BAC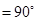 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC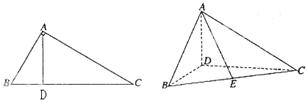
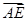 与
与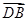 夹角的余弦值.
夹角的余弦值.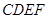 为正方形,面
为正方形,面 为等腰梯形,
为等腰梯形,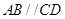 ,
,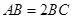 ,
,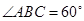 ,且平面
,且平面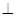 平面
平面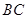 与平面
与平面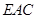 所成角的正弦值;
所成角的正弦值;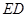 上是否存在点
上是否存在点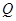 ,使平面
,使平面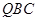 ?
?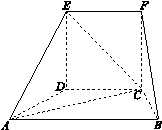
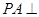 底面ABCD,
底面ABCD,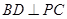 ,E是PA的中点.
,E是PA的中点.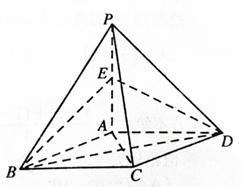
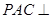 平面EBD;
平面EBD;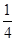 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.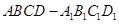 中,
中,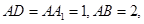 点
点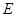 在棱
在棱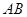 上.
上.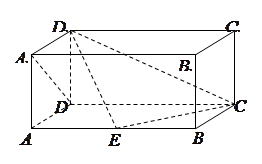
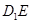 与
与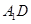 所成的角;
所成的角;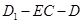 的大小为
的大小为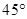 ,求点
,求点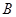 到平面
到平面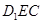 的距离.
的距离.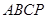 中,
中,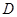 为
为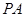 的中点,
的中点,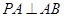 ,
,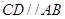 ,
, .将此平面四边形
.将此平面四边形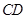 折成直二面角
折成直二面角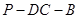 ,
,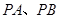 ,设
,设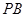 中点为
中点为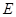 .
.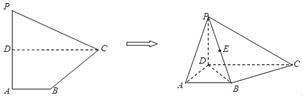
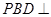 平面
平面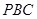 ;
;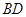 上是否存在一点
上是否存在一点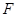 ,使得
,使得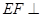 平面
平面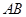 与平面
与平面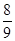 ,则λ=________.
,则λ=________.