题目内容
已知数列an=
,则数列{an}中最大的项为( )
| n |
| n2+156 |
| A.12 | B.13 | C.12或13 | D.不存在 |
考察函数f(x)=
(x>0)的单调性,
f′(x)=
,令f′(x)=0,解得x=
.
∴当x∈(0,
)时,f′(x)>0,此时函数f(x)单调递增;当x∈(
,+∞)时,f′(x)<0,此时函数f(x)单调递减.
又12<
<13.f(12)=f(13)=
.
故当n=12或13时,an取得最大值.
故选:C.
| x |
| x2+156 |
f′(x)=
| -x2+156 |
| (x2+156)2 |
| 156 |
∴当x∈(0,
| 156 |
| 156 |
又12<
| 156 |
| 1 |
| 25 |
故当n=12或13时,an取得最大值.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足:
满足: 且
且 ,则
,则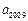 等于( )
等于( )



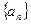 的前
的前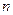 项和
项和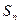 ,分别求它们的通项公式
,分别求它们的通项公式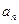 .
.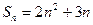 ; ⑵
; ⑵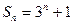 .
.
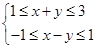 ,则
,则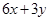 的取值范围是________.
的取值范围是________.