题目内容
已知数列an=1+
+
+…+
，则ak+1-ak共有（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n2 |
| A．1项 | B．k项 | C．2k项 | D．2k+1项 |
∵ak=1+
+
+…+
，ak+1=1+
+
+…+
+
+…+
，
∴ak+1-ak=
+…+
=
+
+…+
，
∴共有k2+2k+1-（k2+1）+1=2k+1项．
故选D．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k2 |
| 1 |
| k2+1 |
| 1 |
| (k+1)2 |
∴ak+1-ak=
| 1 |
| k2+1 |
| 1 |
| (k+1)2 |
| 1 |
| k2+1 |
| 1 |
| k2+2 |
| 1 |
| k2+2k+1 |
∴共有k2+2k+1-（k2+1）+1=2k+1项．
故选D．
练习册系列答案
名校课堂系列答案
相关题目
，
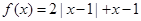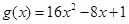，记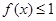
的解集为M，
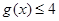的解集为N.
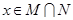时，证明：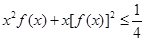
.
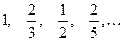的一个通项公式是 。
，
，
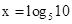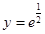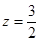，（e是自然对数的底数），则
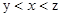
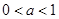时，关于
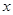的不等式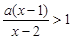
的解集是（ ）
