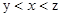题目内容
数列{an}的前n项和为Sn=n2+3n+1,则它的通项公式为______.
由数列{an}的前n项和为Sn=n2+3n+1,
当n=1时,a1=S1=5;
当n≥2时,an=Sn-Sn-1=n2+3n+1-[(n-1)2+3(n-1)+1]
=2n+2.
当n=1时上式不成立.
∴an=
.
故答案为:an=
.
当n=1时,a1=S1=5;
当n≥2时,an=Sn-Sn-1=n2+3n+1-[(n-1)2+3(n-1)+1]
=2n+2.
当n=1时上式不成立.
∴an=
|
故答案为:an=
|

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
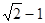 ,B=
,B=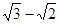 ,C=
,C=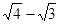
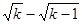 与
与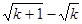 (
(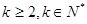 )的大小,并加以证明.
)的大小,并加以证明.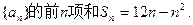 (1)求数列
(1)求数列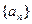 的通项公式;(2)求数列
的通项公式;(2)求数列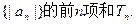
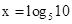 ,
,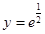 ,
,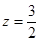 ,(e是自然对数的底数),则
,(e是自然对数的底数),则