题目内容
圆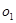 :
: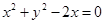 与圆
与圆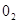 :
: 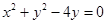 的位置关系是
的位置关系是
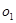 :
: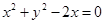 与圆
与圆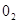 :
: 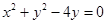 的位置关系是
的位置关系是| A.相离 | B.相交 | C.外切 | D.内切 |
B
分析:把两圆的方程化为标准方程,分别找出圆心坐标和半径,利用两点间的距离公式,求出两圆心的距离d,然后求出R-r和R+r的值,判断d与R-r及R+r的大小关系即可得到两圆的位置关系.
解答:解:把圆
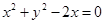 与圆
与圆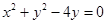 分别化为标准方程得:
分别化为标准方程得:(x-1)
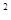 +y
+y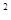 =1,x
=1,x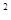 +(y+2)
+(y+2)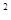 =4,
=4,故圆心坐标分别为(1,0)和(0,-2),半径分别为R=2和r=1,
∵圆心之间的距离d=
 =
=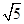 ,R+r=3,R-r=1,
,R+r=3,R-r=1,∴R-r<d<R+r,
则两圆的位置关系是相交.
故选B
点评:圆与圆的位置关系有五种,分别是:当0≤d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆外离(其中d表示两圆心间的距离,R,r分别表示两圆的半径).

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
 B = 90°,AC = 4,BC =
B = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以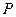 为圆心,1为半径作
为圆心,1为半径作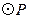 .
.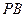 ,若
,若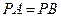 ,试判断
,试判断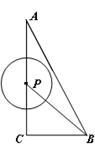
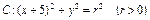 和直线
和直线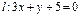 . 若圆
. 若圆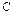 与直线
与直线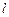 没有公共点,则
没有公共点,则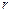 的取值范围是
的取值范围是  与圆
与圆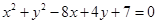 的公切线有 ( )
的公切线有 ( ) 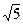 ,1)直线
,1)直线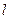 :
: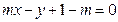
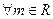 ,直线
,直线 点;
点;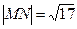 时,求m的值。
时,求m的值。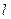 过点
过点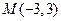 ,圆
,圆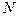 :
: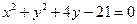 .
. 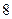 ,求直线
,求直线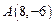 与圆
与圆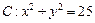 ,
,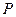 是圆
是圆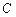 上任意一点,则
上任意一点,则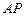 的最小值
的最小值
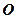 的方程为
的方程为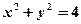 ,
,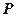 是圆
是圆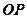 的垂直平分线总是被平面区域
的垂直平分线总是被平面区域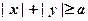 覆盖,则实数
覆盖,则实数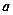 的取值围是 。
的取值围是 。