题目内容
圆 与圆
与圆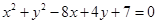 的公切线有 ( )
的公切线有 ( )
 与圆
与圆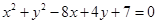 的公切线有 ( )
的公切线有 ( ) | A.4条 | B.3条 | C.2条 | D.1条 |
B
分析:将圆的方程化为标准方程,求出圆心距及半径,可得两圆相外切,由此可确定两圆的公切线的条数.
解答:解:圆C1:x2+y2+4x-4y-5=0化为标准方程为:(x+2)2+(y-2)2=13,圆心坐标为C1(-2,2),半径为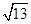
圆C2:x2+y2-8x+4y+7=0化为标准方程为:(x-4)2+(y+2)2=13,圆心坐标为C2(4,-2),半径为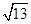
∴圆心距|C1C2|=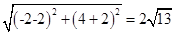
即两圆的圆心距等于两圆的半径的和
∴两圆相外切
∴两圆的公切线有3条
故选B.
点评:本题重点考查两圆的位置关系,考查相外切,解题的关键是确定圆的圆心与半径,属于基础题.
解答:解:圆C1:x2+y2+4x-4y-5=0化为标准方程为:(x+2)2+(y-2)2=13,圆心坐标为C1(-2,2),半径为
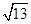
圆C2:x2+y2-8x+4y+7=0化为标准方程为:(x-4)2+(y+2)2=13,圆心坐标为C2(4,-2),半径为
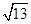
∴圆心距|C1C2|=
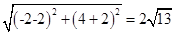
即两圆的圆心距等于两圆的半径的和
∴两圆相外切
∴两圆的公切线有3条
故选B.
点评:本题重点考查两圆的位置关系,考查相外切,解题的关键是确定圆的圆心与半径,属于基础题.

练习册系列答案
相关题目
 +2x-4y=0的圆心,则a的值为
+2x-4y=0的圆心,则a的值为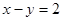 被圆
被圆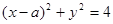 截得弦长为
截得弦长为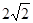 ,则实数
,则实数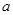 的值为( )
的值为( )
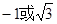
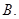
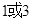
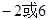

 :
: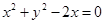 与圆
与圆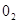 :
: 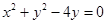 的位置关系是
的位置关系是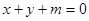 与圆
与圆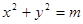 相切,则
相切,则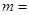 ( )
( )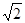
 2个小题,第1小题满分6分,第2小题满分8分.
2个小题,第1小题满分6分,第2小题满分8分. 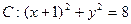 .
. 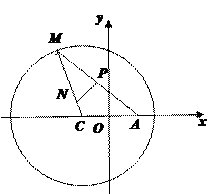
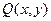 是圆C上一点,求
是圆C上一点,求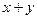 的取值范围;
的取值范围;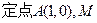 为圆C上一动点,点P在AM上,点N在CM上,且满足
为圆C上一动点,点P在AM上,点N在CM上,且满足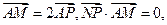 求
求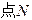 的轨迹的内接矩形的
的轨迹的内接矩形的 最大面积.
最大面积.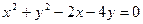 的圆心到直线
的圆心到直线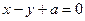 的距离为
的距离为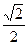 ,则a的值
,则a的值