题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1) 当![]() 时,
时, ![]() 在
在![]() 上单调递减;当
上单调递减;当![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间是
;单调递减区间是![]() 和
和![]() ;当
;当![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求出![]() 的导数,通过
的导数,通过![]() 的讨论,分别令
的讨论,分别令![]() 得增区间,
得增区间, ![]() 得减区间;(2)由题意可得
得减区间;(2)由题意可得![]() 恒成立,令
恒成立,令![]() ,求出导数,确定函数的单调性,可得函数的最值,即可得到结论.
,求出导数,确定函数的单调性,可得函数的最值,即可得到结论.
试题解析:(1)![]() ,
,
![]() ,
,
①当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递减;
上单调递减;
②当![]() ,由
,由![]() 解得
解得![]() ,∴
,∴![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间是![]() 和
和![]() ;
;
③当![]() ,同理可得
,同理可得![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间是
,单调递减区间是![]() 和
和![]() .
.
(2)∵![]() 恒成立,∴
恒成立,∴![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
![]() ,
,
∴![]() 在
在![]() 上递增,
上递增, ![]() 上递减,∴
上递减,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
令![]() ,
,
∴![]() 在
在![]() 上递增,
上递增, 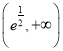 上递减,
上递减,
∴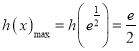 ,∴
,∴![]() ,∴实数
,∴实数![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
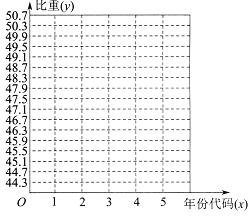
【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
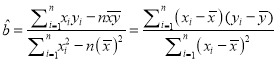 ,
, ![]() .
.