Question

【题目】已知函数.

判断的奇偶性，并作出函数的图像；

关于的方程恰有个不同的实数解，求的取值范围.

Answer 1

【答案】（1）是偶函数；（2）

【解析】

（1）由得，对需分四个范围进行讨论，分别是，，，，可得函数的解析式，再做出其图像；

（2）令，由函数的图像得出，则关于的方程需有两个根，并且一根为，另一根在之间，再根据一元二次方程的根的分布得出不等式组，可得解.

由题意得函数的定义域为，

由，得是偶函数，

因为，所以对分四个范围进行讨论，

当时，，所以；

当时，，所以；

当时，，所以；

当时，，所以；

所以函数，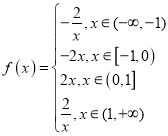

关于的方程恰有个不同的实数解，

即有个不同的解，数形结合可知必有和，，

令，则关于的方程有两个根，并且一根为，另一根在间，则需满足

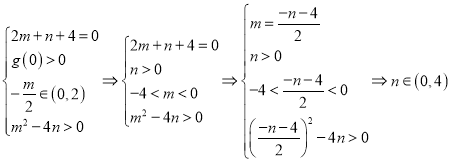
所以的取值范围是.

故得解.