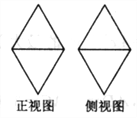
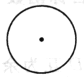
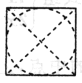
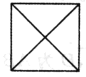
题目内容
【题目】在矩形
中，
，
，点
是线段
上靠近点
的一个三等分点，点
是线段
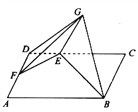
上的一个动点，且
.如图，将
沿
折起至
，使得平面
平面
.
（1）当
时，求证：
；
（2）是否存在
，使得
与平面
所成的角的正弦值为
？若存在，求出的值；若不存在，请说明理由.
【答案】(1)见解析(2) 
【解析】试题分析: (1) 当时，点
是
的中点,由已知证出
,根据面面垂直的性质定理证得
平面
,进而证得结论;(2) 以
为原点，
的方向为
轴，
轴的正方向建立如图所示空间直角坐标系
.写出各点坐标,求出平面
的法向量,根据线面角的公式求出结果.
试题解析:
（1）当时，点是的中点.
∴
，
.
∵
，∴
.
∵
，
，
，
∴
.
∴.
又平面
平面
，平面
平面
，
平面，
∴平面.
∵
平面，∴
.
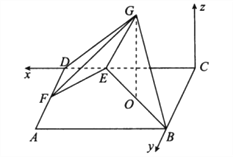
（2）以为原点，的方向为轴，轴的正方向建立如图所示空间直角坐标系.
则
，
，
.
取
的中点
，
∵
，∴
，
∴ 易证得
平面
，
∵
，∴
，∴
.
∴
，
，
.
设平面的一个法向量为
，
则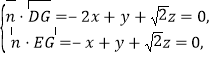
令
，则
.
设
与平面所成的角为
，
则
，
解得或
（舍去）
∴存在实数
，使得
与平面所成的角的正弦值为
，此时.
【题目】《最强大脑》是江苏卫视引进德国节目《SuperBrain》而推出的大型科学竞技真人秀节目.节目筹备组透露挑选选手的方式：不但要对空间感知、照相式记忆进行考核，而且要让选手经过名校最权威的脑力测试，120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关，在该高校随机抽取男、女学生各100名，然后对这200名学生进行脑力测试.规定：分数不小于120分为“入围学生”，分数小于120分为“未入围学生”.已知男生入围24人，女生未入围80人.
（1）根据题意，填写下面的
列联表，并根据列联表判断是否有
以上的把握认为脑力测试后是否为“入围学生”与性别有关；
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | ||
女生 | 80 | ||
总计 |
（2）用分层抽样的方法从“入围学生”中随机抽取11名学生，然后再从这11名学生中抽取3名参加某期《最强大脑》，设抽到的3名学生中女生的人数为
，求的分布列及数学期望.
附：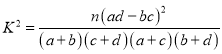
，其中
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】铁人中学高二学年某学生对其亲属30人
饮食习惯进行了一次调查，并用如图所示的茎叶图表示30人的饮食指数．（说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主．）
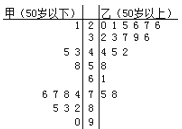
（Ⅰ）根据茎叶图，帮助这位学生说明其亲属30人的饮食习惯；
（Ⅱ）根据以上数据完成下列
的列联表：
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
（Ⅲ）能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系？
附：
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
