Question

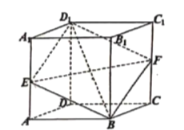
【题目】如图所示，直平行六面体的所有棱长都为2，，过体对角线的截面S与棱和分别交于点E、F，给出下列命题中：

①四边形的面积最小值为；

②直线EF与平面所成角的最大值为；

③四棱锥的体积为定值；

④点到截面S的距离的最小值为.

其中，所有真命题的序号为（ ）

A.①②③B.①③④C.①③D.②④

Answer 1

【答案】B

【解析】

①分析可得当为为棱的中点时,四边形的面积最小,求解即可；

②过点的平面的垂线交平面于点,转化直线EF与平面所成角最大为直线与直线的夹角最小,进而求解即可；

③转化四棱锥的体积为以平面和平面为底的三棱锥的体积的和,进而求证即可；

④分析可得当点与点重合,点与点重合时四边形的面积最大,此时点到截面S的距离的最小,进而求解即可

由题,因为过体对角线,则由对称性易得四边形是平行四边形,

连接,,且交于点,过点作的垂线,垂足为,

则若四边形面积最小,即最小,

即为棱到平面的距离,即为长,

因为,则,

所以,

则,

又,

所以,此时为棱的中点,故①正确；

过点的平面的垂线交平面于点,则即为点到平面的距离,根据底面菱形的性质,可得,

若直线EF与平面所成角最大,则直线与直线的夹角最小,即最小,此时最大,即最小,

即时,故,则,

则直线EF与平面所成角最大为,故②错误；

设点到平面,平面的距离分别为,即从点分别向作垂线即可,由菱形可得,

,

为定值,故③正确；

因为四棱锥的体积为定值,

所以若点到截面S的距离的最小,则截面的面积最大,即四边形面积最大,即最大,则当点与点重合,点与点重合时符合条件,此时在中,,,则,则,

所以,此时,

设点到截面S的距离为,则,所以,故④正确

综上,①③④正确,

故选：B