题目内容
15. 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;
(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
分析 (Ⅰ)证明AE⊥BB1,AE⊥BC,BC∩BB1=B,推出AE⊥平面B1BCC1,利用平面余平米垂直的判定定理证明平面AEF⊥平面B1BCC1;
(Ⅱ)取AB的中点G,说明直线A1C与平面A1ABB1所成的角为45°,就是∠CA1G,求出棱锥的高与底面面积即可求解几何体的体积.
解答 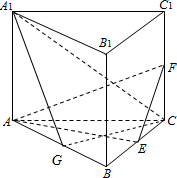 (Ⅰ)证明:∵几何体是直棱柱,∴BB1⊥底面ABC,AE?底面ABC,∴AE⊥BB1,
(Ⅰ)证明:∵几何体是直棱柱,∴BB1⊥底面ABC,AE?底面ABC,∴AE⊥BB1,
∵直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E分别是BC的中点,
∴AE⊥BC,BC∩BB1=B,∴AE⊥平面B1BCC1,
∵AE?平面AEF,∴平面AEF⊥平面B1BCC1;
(Ⅱ)解:取AB的中点G,连结A1G,CG,由(Ⅰ)可知CG⊥平面A1ABB1,
直线A1C与平面A1ABB1所成的角为45°,就是∠CA1G,则A1G=CG=$\sqrt{3}$,
∴AA1=$\sqrt{{A}_{1}{G}^{2}-{AG}^{2}}$=$\sqrt{2}$,CF=$\frac{\sqrt{2}}{2}$.
三棱锥F-AEC的体积:$\frac{1}{3}$×$\frac{1}{2}×CE•AE•CF$=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{3}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{12}$.
点评 本题考查几何体的体积的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
5.若等比数列{an}中,a2+a5+a11=2,a5+a8+a14=6,则a2+a5+a8+a11+a14的值为( )
| A. | 8 | B. | 大于8 | C. | $\frac{242}{31}$ | D. | $\frac{240}{41}$ |
10.某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=$\frac{新工件的体积}{原工件的体积}$)( )


| A. | $\frac{8}{9π}$ | B. | $\frac{8}{27π}$ | C. | $\frac{24(\sqrt{2}-1)^{3}}{π}$ | D. | $\frac{8(\sqrt{2}-1)^{3}}{π}$ |
20.过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=( )
| A. | 2$\sqrt{6}$ | B. | 8 | C. | 4$\sqrt{6}$ | D. | 10 |
4.已知复数z满足(z-1)i=1+i,则z=( )
| A. | -2-i | B. | -2+i | C. | 2-i | D. | 2+i |
 高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.
高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生. 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.