已知ABCD-A1B1C1D1是棱长为a的正方体.求DA1与平面AA1BB1所成的角．题目和参考答案——青夏教育精英家教网—

题目内容

20．已知ABCD-A₁B₁C₁D₁是棱长为a的正方体，求DA₁与平面AA₁BB₁所成的角．

分析根据直线和平面所成角的定义，进行求解即可．

解答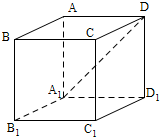解：∵AD⊥AA₁BB₁，
∴AA₁是DA₁在AA₁BB₁上的射影，
即∠AA₁D是DA₁与平面AA₁BB₁所成的角．
解得∠AA₁D=45°，
即DA₁与平面AA₁BB₁所成的角为45°．

点评本题主要考查直线和平面所成角的求解，根据定义找出直线和平面所成角的平面角是解决本题的关键．

练习册系列答案

11．甲乙两人进行围棋比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止．设甲在每局中获胜的概率为$p（{p＞\frac{1}{2}}）$，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$．
（Ⅰ）求p的值；
（Ⅱ）设X表示比赛停止时已比赛的局数，求随机变量X的分布列和数学期望EX．

8．

如图的矩形长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，由此我们可以估计出阴影部分的面积约为4.6．

15．设函数f（x）=2+$\frac{2mx+sinx+mxcosx}{2+cosx}$，若f（x）在[-n，n]上的值域为[a，b]，其中a，b，m，n∈R，且n＞0，则a+b=4．

5．若等比数列{a_n}中，a₂+a₅+a₁₁=2，a₅+a₈+a₁₄=6，则a₂+a₅+a₈+a₁₁+a₁₄的值为（　　）

12．若x∈R，则函数f（x）=3-3sinx-cos²x的最大值，最小值分别为（　　）

	A．	最小值为0，无最大值		B．	最小值为0，最大值为6
	C．	最小值为-$\frac{1}{4}$，无最大值		D．	最小值为-$\frac{1}{4}$，最大值为6

9．

如图，三棱台DEF-ABC中，AB=2DE，G，H分别为AC，BC的中点．
（1）求证：BD∥平面FGH；
（2）若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH．

10．某工件的三视图如图所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=$\frac{新工件的体积}{原工件的体积}$）（　　）

$\frac{24（\sqrt{2}-1）^{3}}{π}$

D．

$\frac{8（\sqrt{2}-1）^{3}}{π}$

试题分类