题目内容
【题目】已知椭圆E: ![]() =1(a>b>0)上任意一点到两焦点距离之和为
=1(a>b>0)上任意一点到两焦点距离之和为 ![]() ,离心率为
,离心率为 ![]() ,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
(1)求椭圆E的标准方程;
(2)证明:直线PQ与直线OQ的斜率之积是定值;
(3)证明:直线PQ与椭圆E只有一个公共点.
【答案】
(1)解:由题意可得 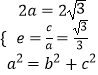 ,解得
,解得 ![]() ,c=1,
,c=1, ![]()
所以椭圆E: ![]() .
.
(2)解:由(1)可知:椭圆的右准线方程为 ![]() ,
,
设P(3,y0),Q(x1,y1),
因为PF2⊥F2Q,所以 ![]() ,
,
所以﹣y1y0=2(x1﹣1)
又因为 ![]() 且
且 ![]() 代入化简得
代入化简得 ![]() .
.
即直线PQ与直线OQ的斜率之积是定值 ![]()
(3)解:由(2)知, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∴直线PQ的方程为 ![]() ,即
,即 ![]() ,
,
联立 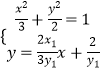 得
得 ![]() ,
,
∵ ![]() ,
, ![]() .
.
∴化简得: ![]() ,又△=0,
,又△=0,
解得x=x1,所以直线PQ与椭圆C相切,只有一个交点
【解析】(1)由题意可得 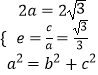 ,解出即可;(2)由(1)可知:椭圆的右准线方程为
,解出即可;(2)由(1)可知:椭圆的右准线方程为 ![]() ,设P(3,y0),Q(x1 , y1),由PF2⊥F2Q,可得
,设P(3,y0),Q(x1 , y1),由PF2⊥F2Q,可得 ![]() ,利用斜率计算公式可得kPQkOQ及
,利用斜率计算公式可得kPQkOQ及 ![]() 代入化简得直线PQ与直线OQ的斜率之积是定值.(3)由(2)知,直线PQ的方程为
代入化简得直线PQ与直线OQ的斜率之积是定值.(3)由(2)知,直线PQ的方程为 ![]() ,即
,即 ![]() ,与椭圆的方程联立,消去一个未知数得到关于x的一元二次方程,只要证明△=0即可.
,与椭圆的方程联立,消去一个未知数得到关于x的一元二次方程,只要证明△=0即可.
【考点精析】关于本题考查的直线的斜率和椭圆的标准方程,需要了解一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目