题目内容
【题目】设函数f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的对边分别为A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
【答案】(1)周期为π,最大值为2.(2)![]()
【解析】
(1)利用倍角公式降幂,展开两角差的余弦,将函数的关系式化简余弦型函数,可求出函数的周期及最值;
(2)由f(π﹣A)![]() ,求解角A,再利用余弦定理和基本不等式求a的最小值.
,求解角A,再利用余弦定理和基本不等式求a的最小值.
(1)函数f(x)=2cos2x﹣cos(2x![]() )
)
=1+cos2x![]()
=cos(2x![]() )+1,
)+1,
∵﹣1≤cos(2x![]() )≤1,
)≤1,
∴T![]() ,f(x)的最大值为2;
,f(x)的最大值为2;
(2)由题意,f(π﹣A)=f(﹣A)=cos(﹣2A![]() )+1
)+1![]() ,
,
即:cos(﹣2A![]() )
)![]() ,
,
又∵0<A<π,
∴![]() 2A
2A![]() ,
,
∴﹣2A![]() ,即A
,即A![]() .
.
在△ABC中,b+c=2,cosA![]() ,
,
由余弦定理,a2=b2+c2﹣2bccosA=(b+c)2﹣bc,
由于:bc![]() ,当b=c=1时,等号成立.
,当b=c=1时,等号成立.
∴a2≥4﹣1=3,即a![]() .
.
则a的最小值为![]() .
.

【题目】某生产企业研发了一种新产品,该产品在试销一个阶段后得到销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:万件)之间的一组数据,如下表所示:
(单位:万件)之间的一组数据,如下表所示:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)从反馈的信息来看,消费者对该产品的心理价(单位:元/件)在![]() 内,已知该产品的成本是
内,已知该产品的成本是![]() 元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
参考数据:![]()
参考公式: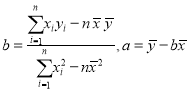
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
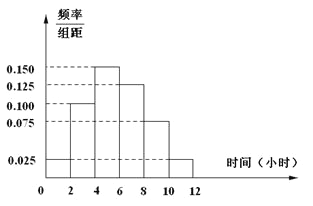
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】某种机器零件转速在符合要求的范围内使用时间随机器运转速度的变化而变化,某检测员随机收集了20个机器零件的使用时间与转速的数据,列表如下:
机器转速(转/分) | 189 | 193 | 190 | 185 | 183 | 202 | 187 | 203 | 192 | 201 |
零件使用时间(月) | 43 | 33 | 39 | 37 | 38 | 37 | 38 | 35 | 38 | 35 |
机器转速(转/分) | 193 | 197 | 191 | 186 | 191 | 188 | 185 | 204 | 201 | 189 |
零件使用时间(月) | 37 | 40 | 41 | 37 | 35 | 37 | 42 | 36 | 34 | 40 |
(Ⅰ)若“转速大于200转/分”为“高速”,“转速不大于200转/分”为“非高速”,“使用时间大于36个月”的为“长寿命”,“使用时间不大于36个月”的为“非长寿命”,请根据上表数据完成下面的![]() 列联表:
列联表:
高速 | 非高速 | 合计 | |
长寿命 | |||
非长寿命 | |||
合计 |
(Ⅱ)根据(Ⅰ)中的![]() 列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |