题目内容
设奇函数f(x)在[－1，1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1，1]都成立，则当a∈[－1，1]时t的取值范围是( )
| A．－2≤t≤2 | B．－ ≤t≤ |
| C．t≤－2或t＝0或t≥2 | D．t≤－或t＝0或t≥ |
C
解析
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
的对角线
上任取一点P，以
为球心，
为半径作一个球.设
，记该球面与正方体表面的交线的长度和为
，则函数
已知函数
，若
互不相等，且
，则
的取值范围是（ ）
A． | B． | C． | D． |
若函数
在
上单调递增，则实数
的取值范围( )
A． | B． | C． | D． |
函数f(x)=
+lg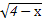
的定义域是( )
| A．(2,4) | B．(3,4) |
| C．(2,3)∪(3,4] | D．[2,3)∪(3,4) |
已知函数f(x)的图像如图所示，则f(x)的解析式可以是( )
A．f(x)＝x－ | B．f(x)＝ | C．f(x)＝ －1 | D．f(x)＝ |
函数f(x)＝1－xlog2x的零点所在的区间是( )
A． ， | B．，1 | C．(1，2) | D．(2，3) |
已知f(x)是定义在(0，＋∞) 上的非负可导函数，且满足xf′(x)＋f(x)≤0，对任意的0<a<b，则必有( )．
| A．af(b)≤bf(a) | B．bf(a)≤af(b) |
| C．af(a)≤f(b) | D．bf(b)≤f(a) |