题目内容
函数f(x)=
+lg
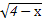的定义域是( )
| A．(2,4) | B．(3,4) |
| C．(2,3)∪(3,4] | D．[2,3)∪(3,4) |
D
解析
练习册系列答案
阅读快车系列答案
相关题目
定义域为
的偶函数
满足对
，有
，且当
时，
，若函数
至少有三个零点，则
的取值范围是( )
A． | B． | C． | D． |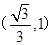
已知函数f(x)＝
若关于x的方程f(f(x))＝0有且仅有一个实数解，则实数a的取值范围是( )
| A．(－∞，0) | B．(－∞，0)∪(0,1) |
| C．(0,1) | D．(0,1)∪(1，＋∞) |
已知定义在R上的函数y＝f(x)满足下列三个条件：①对任意的x∈R都有f(x＋2)＝－f(x)；②对于任意的0≤x1<x2≤2，都有f(x1)<f(x2)；③y＝f(x＋2)的图像关于y轴对称．下列结论中，正确的是( )
| A．f(4.5)<f(6.5)<f(7) |
| B．f(4.5)<f(7)<f(6.5) |
| C．f(7)<f(4.5)<f(6.5) |
| D．f(7)<f(6.5)<f(4.5) |
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
| A．(-∞,-1)∪(2,+∞) |
| B．(-1,2) |
| C．(-2,1) |
| D．(-∞,-2)∪(1,+∞) |
x为实数，[x]表示不超过x的最大整数，则函数f(x)＝x－[x]在R上为( )
| A．奇函数 | B．偶函数 |
| C．增函数 | D．周期函数 |
函数f(x)＝x＋sin x(x∈R)( )
| A．是偶函数且为减函数 |
| B．是偶函数且为增函数 |
| C．是奇函数且为减函数 |
| D．是奇函数且为增函数 |
设奇函数f(x)在[－1，1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1，1]都成立，则当a∈[－1，1]时t的取值范围是( )
| A．－2≤t≤2 | B．－ ≤t≤ |
| C．t≤－2或t＝0或t≥2 | D．t≤－或t＝0或t≥ |
已知定义在R上的函数y＝f(x)满足以下三个条件：①对于任意的x∈R，都有f(x＋4)＝f(x)；②对于任意的x1，x2∈R，且0≤x1<x2≤2，都有f(x1)＜f(x2)；③函数y＝f(x＋2)的图象关于y轴对称．则下列结论中正确的是( )．
| A．f(4.5)＜f(7)＜f(6.5) | B．f(7)＜f(4.5)＜f(6.5) |
| C．f(7)＜f(6.5)＜f(4.5) | D．f(4.5)＜f(6.5)＜f(7) |