题目内容
如图,在棱长为1的正方体 的对角线
的对角线 上任取一点P,以
上任取一点P,以 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数 的图象最有可能的是( )
的图象最有可能的是( )
A
解析试题分析:分析:当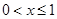 ,以
,以 为半径的球面与正方体
为半径的球面与正方体 的侧面
的侧面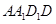 、
、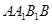 以及下底面
以及下底面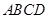 均相交,且与侧面
均相交,且与侧面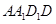 、
、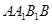 以及下底面
以及下底面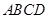 的交线均为圆心角为
的交线均为圆心角为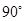 的圆弧,即
的圆弧,即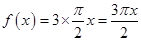 ,此时函数
,此时函数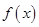 是关于自变量
是关于自变量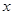 的正比例函数,排除选项
的正比例函数,排除选项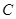 、
、 ,当
,当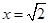 时,侧面
时,侧面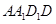 、
、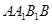 以及下底面
以及下底面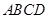 内的点到点
内的点到点 的最大距离为
的最大距离为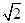 ,此时球面与这三个面无交线,考虑球面与平面
,此时球面与这三个面无交线,考虑球面与平面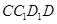 的交线,设球面与平面
的交线,设球面与平面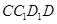 的交线是半径为
的交线是半径为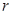 的圆弧,在圆弧上任取一点
的圆弧,在圆弧上任取一点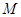 ,则
,则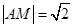 ,
,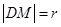 ,易知,
,易知,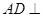 平面
平面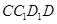 ,由于
,由于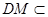 平面
平面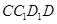 ,
,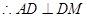 ,由勾股定理得
,由勾股定理得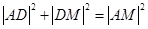 ,则有
,则有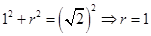 ,即球面与正方体的侧面
,即球面与正方体的侧面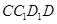 的交线为以
的交线为以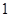 为半径,且圆心角为
为半径,且圆心角为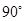 的圆弧,同理,球面与侧面
的圆弧,同理,球面与侧面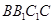 及底面
及底面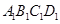 的交线都是以
的交线都是以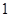 为半径,且圆心角为
为半径,且圆心角为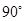 的圆弧,即
的圆弧,即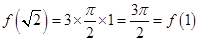 ,排除
,排除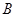 选项,故选项
选项,故选项 正确.
正确.
考点:1弧长公式;2函数图像及表示法。

定义域为 的偶函数
的偶函数 满足对
满足对 ,有
,有 ,且当
,且当 时,
时, ,若函数
,若函数 至少有三个零点,则
至少有三个零点,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.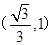 |
已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
| A.[1,+∞) | B.[0,2] |
| C.[1,2] | D.(-∞,2] |
若函数y=f(x)(x∈R)满足f(x+1)=f(x-1),且x∈[-1,1]时,f(x)=1-x2,函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
| A.6 | B.7 | C.8 | D.9, |
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时t的取值范围是( )
| A.-2≤t≤2 | B.- ≤t≤ ≤t≤ |
| C.t≤-2或t=0或t≥2 | D.t≤- 或t=0或t≥ 或t=0或t≥ |
已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则 ( ).
| A.a>0,4a+b=0 | B.a<0,4a+b=0 |
| C.a>0,2a+b=0 | D.a<0,2a+b=0 |
已知函数f(x)=ax+x-b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足2a=3,3b=2.则n的值是 ( ).
| A.-2 | B.-1 | C.0 | D.1 |
函数f(x)=2ln x的图象与函数g(x)=x2-4x+5的图象的交点个数为( ).
| A.3 | B.2 | C.1 | D.0 |
已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-3,则f(-2)=( ).
| A.1 | B.-1 | C. | D.- |