题目内容
(本小题满分10分)
已知数列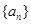 满足
满足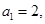 且对任意
且对任意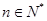 ,恒有
,恒有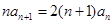
(1) 求数列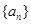 的通项公式;
的通项公式;
(2) 设区间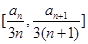 中的整数个数为
中的整数个数为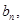 求数列
求数列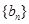 的通项公式。
的通项公式。
已知数列
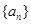 满足
满足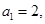 且对任意
且对任意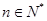 ,恒有
,恒有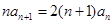
(1) 求数列
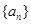 的通项公式;
的通项公式;(2) 设区间
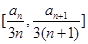 中的整数个数为
中的整数个数为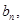 求数列
求数列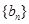 的通项公式。
的通项公式。⑴ .
.
⑵ 当 为奇数时,
为奇数时,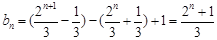 ;
;
当 为偶数时,
为偶数时,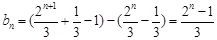 .
.
 .
.⑵ 当
 为奇数时,
为奇数时,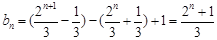 ;
;当
 为偶数时,
为偶数时,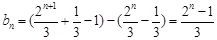 .
.本试题主要是考查了递推关系式,求解数列的通项公式,并能运用数列的通项公式的特点,合理的选用求和的方法,运用整体思想得到数列的通项公式的求解。
(1)根据已知的递推关系,可以变形得到相邻两项的关系式,然后累积法得到通项公式。
((2)在第一问的基础上可以利用整体的思想,作差法表示得到数列的通项公式。
⑴由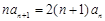 ,得
,得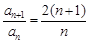 ,当
,当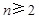 时,
时,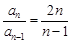 ,
,
所以,当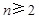 时,
时, ,
,
此式对于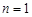 也成立,所以数列
也成立,所以数列 的通项公式为
的通项公式为 .…………………4分
.…………………4分
⑵ 由⑴知, ,
,
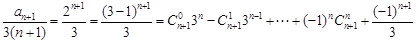 ,……………8分
,……………8分
当 为奇数时,
为奇数时,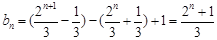 ;
;
当 为偶数时,
为偶数时,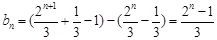 .……………………………10分
.……………………………10分
(1)根据已知的递推关系,可以变形得到相邻两项的关系式,然后累积法得到通项公式。
((2)在第一问的基础上可以利用整体的思想,作差法表示得到数列的通项公式。
⑴由
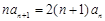 ,得
,得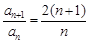 ,当
,当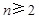 时,
时,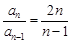 ,
,所以,当
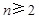 时,
时, ,
,此式对于
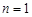 也成立,所以数列
也成立,所以数列 的通项公式为
的通项公式为 .…………………4分
.…………………4分⑵ 由⑴知,
 ,
,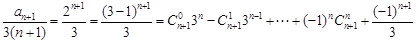 ,……………8分
,……………8分当
 为奇数时,
为奇数时,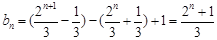 ;
;当
 为偶数时,
为偶数时,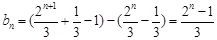 .……………………………10分
.……………………………10分
练习册系列答案
相关题目
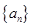 的前n项和为Sn ,且满足
的前n项和为Sn ,且满足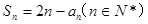 。
。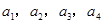 ;
;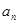 ,并用数学归纳法证明。
,并用数学归纳法证明。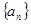 的前
的前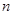 项和
项和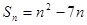 ,且满足
,且满足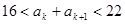 ,则正整数
,则正整数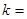 _____
_____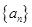 ,
,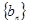 满足:
满足: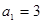 ,当
,当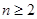 时,
时,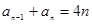 ;对于任意的正整数
;对于任意的正整数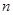 ,
,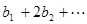
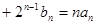 .设数列
.设数列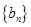 的前
的前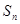 .
.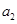 、
、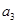 ,并求数列
,并求数列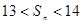 的正整数
的正整数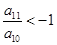 ,且它们的前n项和为Sn有最大值,则使得Sn<0的n的最小值为( )
,且它们的前n项和为Sn有最大值,则使得Sn<0的n的最小值为( )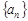 中,
中,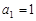 ,
,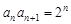
 ,则数列
,则数列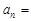 .
. 的通项公式为
的通项公式为 , 则它的公差为 ( )
, 则它的公差为 ( )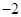
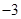
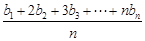 (n∈N*),求数列{bn}的通项公式.
(n∈N*),求数列{bn}的通项公式.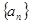 的前
的前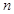 项和为
项和为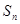 ,已知
,已知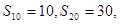 ,则
,则