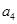题目内容
数列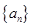 的前n项和为Sn ,且满足
的前n项和为Sn ,且满足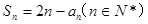 。
。
(Ⅰ)计算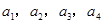 ;
;
(Ⅱ)猜想通项公式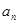 ,并用数学归纳法证明。
,并用数学归纳法证明。
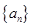 的前n项和为Sn ,且满足
的前n项和为Sn ,且满足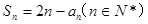 。
。(Ⅰ)计算
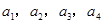 ;
;(Ⅱ)猜想通项公式
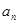 ,并用数学归纳法证明。
,并用数学归纳法证明。(Ⅰ)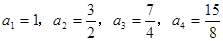 (Ⅱ)见解析
(Ⅱ)见解析
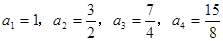 (Ⅱ)见解析
(Ⅱ)见解析本试题主要是考查了数列的通项公式的求解,以及运用归纳猜想的思想得到通项公式,并运用数学归纳法加以证明的综合运用。
(1)利用前n项和的关系式,对于n令值,就可以得到数列的前几项。
(2)结合前几项的规律,归纳猜想其通项公式,然后运用数学归纳法分为两步骤求解得到结论。
解:(Ⅰ)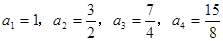 …………………4分
…………………4分
(Ⅱ)猜想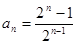 ,证明:
,证明:
① 当n="1" 时,a1=1猜想显然成立;………………………7分
② 假设当n=k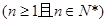 )时,猜想成立,
)时,猜想成立,
即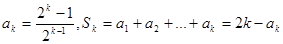 ,
,
那么,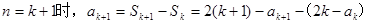 ,
,
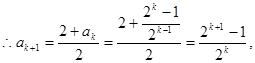
 ………11分
………11分
综合①②,当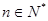 时猜想成立
时猜想成立
(1)利用前n项和的关系式,对于n令值,就可以得到数列的前几项。
(2)结合前几项的规律,归纳猜想其通项公式,然后运用数学归纳法分为两步骤求解得到结论。
解:(Ⅰ)
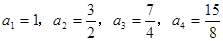 …………………4分
…………………4分(Ⅱ)猜想
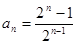 ,证明:
,证明:① 当n="1" 时,a1=1猜想显然成立;………………………7分
② 假设当n=k
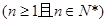 )时,猜想成立,
)时,猜想成立,即
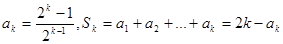 ,
,那么,
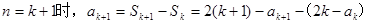 ,
,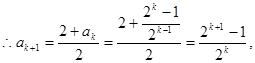
 ………11分
………11分综合①②,当
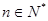 时猜想成立
时猜想成立
练习册系列答案
相关题目
 满足
满足 .
. ,求
,求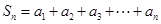 ;
;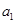 的值,使得数列
的值,使得数列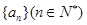 成等差数列.
成等差数列.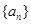 满足
满足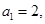 且对任意
且对任意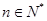 ,恒有
,恒有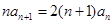
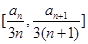 中的整数个数为
中的整数个数为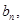 求数列
求数列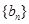 的通项公式。
的通项公式。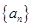 的前
的前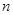 项和为
项和为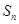 ,已知
,已知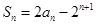 (n∈N*).
(n∈N*).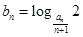 ,数列
,数列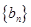 的前
的前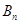 ,若存在整数
,若存在整数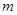 ,使对任意n∈N*且n ≥2,都有
,使对任意n∈N*且n ≥2,都有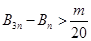 成立,求
成立,求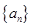 的前
的前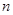 项和为
项和为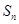 ,且满足
,且满足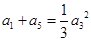 ,
,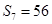 .
.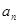 ;
;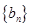 满足
满足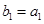 且
且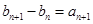 ,求数列
,求数列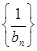 的前
的前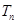 .
.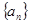 的前
的前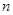 项和为
项和为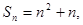
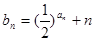 ,求数列
,求数列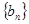 的前
的前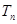 .
.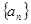 的前n项和为
的前n项和为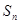 ,
,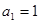 ,
,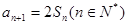
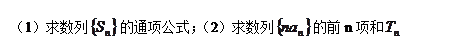
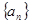 的前
的前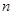 项和
项和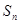 满足
满足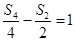 则数列
则数列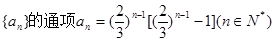 ,则下列表述正确的是
,则下列表述正确的是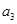
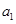 ,最小项不存在
,最小项不存在