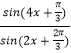题目内容
【题目】如图，矩形ABCD中，AB=2AD=4，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE，构成四棱锥A1﹣BCDE，若M为线段A1C的中点，在翻转过程中有如下4个命题： ①MB∥平面A1DE；
②存在某个位置，使DE⊥A1C；
③存在某个位置，使A1D⊥CE；
④点A1在半径为 
的圆面上运动，
其中正确的命题个数是（ ）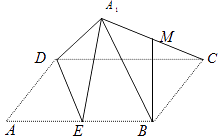
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解：取CD中点F，连接MF，BF，则MF∥DA1 ， BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故①正确 ∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，
∴存在某个位置，使DE⊥A1C不正确，故②不正确．
由CE⊥DE，可得平面A1DE⊥平面ABCD时，A1D⊥CE，故②正确．
∵DE的中点O是定点，OA1= 
，∴A1是在以O为圆心， 为半径的圆上，故④正确，
故选：C．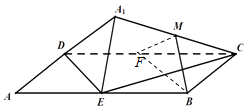
【考点精析】通过灵活运用棱锥的结构特征，掌握侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方即可以解答此题．
练习册系列答案
相关题目
