题目内容
【题目】如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 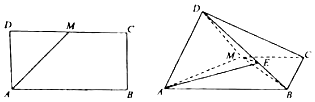
(1)求证:AD⊥BM;
(2)若 ![]() =2
=2 ![]() ,求二面角E﹣AM﹣D的正弦值.
,求二面角E﹣AM﹣D的正弦值.
【答案】
(1)证明:长方形ABCD中,设AB=2,AD=1,M为DC的中点
则AM=BM= ![]() ,∴AM2+BM2=AB2,∴BM⊥AM
,∴AM2+BM2=AB2,∴BM⊥AM
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM平面ABCM
∴BM⊥平面ADM
∵AD平面ADM,∴AD⊥BM
(2)解:建立如图所示的直角坐标系,
∵ ![]() =2
=2 ![]() ,设AB=2,AD=1,
,设AB=2,AD=1,
∴A( ![]() ,0,0),M(﹣
,0,0),M(﹣ ![]() ,0,0),B(﹣
,0,0),B(﹣ ![]() ,
, ![]() ,0),D(0,0,
,0),D(0,0, ![]() ),
),
则平面AMD的一个法向量 ![]() =(0,1,0),
=(0,1,0),
![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,0,0),
,0,0),
设AME的一个法向量 ![]() =(x,y,z),
=(x,y,z),
则 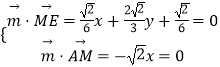 ,取y=1,得
,取y=1,得 ![]() =(0,1,﹣4),
=(0,1,﹣4),
设二面角E﹣AM﹣D的平面角为θ,
则cosθ= ![]() =
= ![]() ,sinθ=
,sinθ= ![]() =
= ![]() ,
,
∴二面角E﹣AM﹣D的正弦值为 ![]() .
.
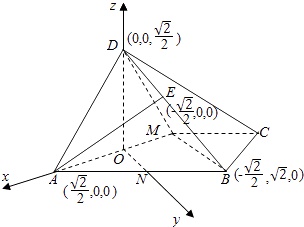
【解析】(1)先证明BM⊥AM,再利用平面ADM⊥平面ABCM,证明BM⊥平面ADM,从而可得AD⊥BM.(2)建立直角坐标系,求出平面AMD、平面AME的一个法向量,利用向量的夹角公式,即可得出二面角E﹣AM﹣D的正弦值.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目