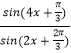题目内容
【题目】已知函数f( ![]() )=﹣
)=﹣ ![]() x3+
x3+ ![]() x2﹣m,g(x)=﹣
x2﹣m,g(x)=﹣ ![]() x3+mx2+(a+1)x+2xcosx﹣m.
x3+mx2+(a+1)x+2xcosx﹣m.
(1)若曲线y=f(x)仅在两个不同的点A(x1 , f(x1)),B(x1 , f(x2))处的切线都经过点(2,t),求证:t=3m﹣8,或t=﹣ ![]() m3+
m3+ ![]() m2﹣m.
m2﹣m.
(2)当x∈[0,1]时,若f(x)≥g(x)恒成立,求a的取值范围.
【答案】
(1)解:证明:由f( ![]() )=﹣
)=﹣ ![]() x3+
x3+ ![]() x2﹣m,可得f(x)=﹣x3+mx2﹣m,
x2﹣m,可得f(x)=﹣x3+mx2﹣m,
f′(x)=﹣3x2+2mx,可得A处的切线方程:y﹣(﹣x13+mx12﹣m)=(﹣3x12+2mx)(x﹣x1),
同理可得B处的切线方程:y﹣(﹣x23+mx22﹣m)=(﹣3x22+2mx)(x﹣x2),
代入点(2,t),可得x1,x2为方程t﹣(﹣x3+mx2﹣m)=(﹣3x2+2mx)(2﹣x)的两个不等实根,
化简整理可得,2x3﹣(m+6)x2+4mx﹣m﹣t=0,
令g(x)=2x3﹣(m+6)x2+4mx﹣m﹣t,g′(x)=6x2﹣2(m+6)x+4m=2(3x﹣m)(x﹣2),
由g′(x)=0,可得x=2或x= ![]() .
.
g(2)=3m﹣8﹣t,g( ![]() )=﹣
)=﹣ ![]() m3+
m3+ ![]() m2﹣m﹣t,
m2﹣m﹣t,
由题意可得g(x)必有一个极值为0,则t=3m﹣8,或t=﹣ ![]() m3+
m3+ ![]() m2﹣m
m2﹣m
(2)解:当x∈[0,1]时,若f(x)≥g(x)恒成立,
即为﹣x3+mx2﹣m≥﹣ ![]() x3+mx2+(a+1)x+2xcosx﹣m,
x3+mx2+(a+1)x+2xcosx﹣m,
即有 ![]() x3+(a+1)x+2xcosx≤0,
x3+(a+1)x+2xcosx≤0,
当x=0时,上式显然成立;
当0<x≤1时,即有﹣a﹣1≥ ![]() x2+2cosx恒成立,
x2+2cosx恒成立,
令m(x)= ![]() x2+2cosx,m′(x)=x﹣2sinx,m′′(x)=1﹣2cosx,
x2+2cosx,m′(x)=x﹣2sinx,m′′(x)=1﹣2cosx,
由0<x≤1时,1<2cos1≤2cosx<2,则1﹣2cosx<0,
y=x﹣2sinx在(0,1]递减,可得x﹣2sinx<0,
则m(x)在(0,1]递减,可得m(x)<m(0)=2,
则﹣a﹣1≥2,解得a≤﹣3.
a的取值范围是(﹣∞,﹣3]
【解析】(1)求出f(x)的导数,可得A,B处的切线方程,代入点(2,t),可得x1 , x2为方程t﹣(﹣x3+mx2﹣m)=(﹣3x2+2mx)(2﹣x)的两个不等实根,化简整理可得,2x3﹣(m+6)x2+4mx﹣m﹣t=0,令g(x)=2x3﹣(m+6)x2+4mx﹣m﹣t,求出导数,由题意可得g(x)必有一个极值为0,计算即可得到证明;(2)由题意可得﹣x3+mx2﹣m≥﹣ ![]() x3+mx2+(a+1)x+2xcosx﹣m,即有
x3+mx2+(a+1)x+2xcosx﹣m,即有 ![]() x3+(a+1)x+2xcosx≤0,讨论x=0,显然成立;当0<x≤1时,运用参数分离和构造函数法,求出导数,判断单调性,求出最值,即可得到所求a的范围.
x3+(a+1)x+2xcosx≤0,讨论x=0,显然成立;当0<x≤1时,运用参数分离和构造函数法,求出导数,判断单调性,求出最值,即可得到所求a的范围.
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).

 阅读快车系列答案
阅读快车系列答案