题目内容

【题目】下列说法：

①函数的图象和直线的公共点个数是，则的值可能是；

②若函数定义域为且满足，则它的图象关于轴对称；

③函数的值域为；

④若函数在上有零点，则实数的取值范围是.

其中正确的序号是_________.

【答案】①③④

【解析】

①：画出函数图像即可得出答案.

②：的函数关于轴对称.

③：讨论的正负号，利用函数的单调性分别求出函数的值域.再求并集即可.

④：讨论二次函数的对称轴的位置，再利用函数的零点分布性质列出不等式，解出即可.

①画出函数的图象，如图所示：

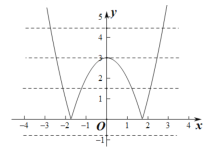
则的值可能是.正确.

②若函数定义域为且满足，则它的图象关于对称,错误.

③函数，

当时，在单调递增，所以

当时，在单调递增，

所以函数的值域为.

④当时函数在上单调递减，在上单调递增.

函数在上有零点等价于： 或

即.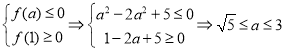

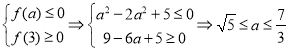
所以.

当时函数在上单调递减。

函数在上有零点等价于：无解.

综上所述：.正确.

故填：①③④

练习册系列答案
相关题目

【题目】已知f(x)是定义在[－4，4]上的奇函数,当x∈(0，4]时,函数的解析式为 (a∈R), 且．

(1)试求a的值；

(2)求f(x)在[-4，4]上的解析式；

(3)求f(x)在[-4，0)上的最值（最大值和最小值）．

【题目】设有三个乡镇，分别位于一个矩形的两个顶点M，N及的中点S处，，现要在该矩形的区域内（含边界），且与M，N等距离的一点O处设一个宣讲站，记O点到三个乡镇的距离之和为．

（1）设，试将L表示为x的函数并写出其定义域；

（2）试利用（1）的函数关系式确定宣讲站O的位置，使宣讲站O到三个乡镇的距离之和最小．

【题目】已知抛物线的焦点为，过点的直线与抛物线交于，两点，线段的垂直平分线交轴于点，若，则点的横坐标为（ ）

A. 5 B. 4 C. 3 D. 2

【题目】已知函数.

（1）当时，求函数在上的最大值；

（2）令，若在区间上为单调递增函数，求的取值范围；

（3）当 时，函数 的图象与轴交于两点 ，且 ，又是的导函数.若正常数 满足条件.证明：.

【题目】已知函数，，，令.

（1）当时，求函数的单调区间及极值；

（2）若关于的不等式恒成立，求整数的最小值.

【题目】已知向量a＝(cosωx－sinωx，sinωx)，b＝(－cosωx－sinωx,2cosωx)．设函数f(x)＝a·b＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈.

(1)求函数f(x)的最小正周期；

(2)若y＝f(x)的图象经过点，求函数f(x)在区间上的取值范围

【题目】已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.

(1)求数列{an}的通项公式；

(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系，将曲线上的每一个点的横坐标保持不变，纵坐标缩短为原来的，得到曲线，以坐标原点为极点， 轴的正半轴为极轴，建立极坐标系， 的极坐标方程为．

（Ⅰ）求曲线的参数方程；

（Ⅱ）过原点且关于轴对称的两条直线与分别交曲线于、和、，且点在第一象限，当四边形的周长最大时，求直线的普通方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网