题目内容

19．以集合A={2，4，6，7，8，11，12，13}中的任意两个元素分别为分子与分母构成分数，则这种分数是可约分数的概率是$\frac{5}{14}$．

分析 分析出共可得到多少个分数，再在其中分析有多少个分子与分母能约分的分数，相比即为所求的概率．

解答 解：因为以A={2，4，6，7，8，11，12，13}中的任意两个元素分别为分子与分母共可构成A82=56个分数，
由于这种分数是可约分数的分子与分母比全为偶数，故这种分数是可约分数的共有A52=20个，
则分数是可约分数的概率为P=$\frac{20}{56}$=$\frac{5}{14}$，
故答案为：$\frac{5}{14}$．

点评 本题主要考查了等可能事件的概率，用到的知识点为：概率=所求情况数与总情况数之比．

练习册系列答案
相关题目
9．已知函数f（x）=$\frac{{4}^{x}}{{4}^{x}+2}$．
（Ⅰ）求f（x）+f（1-x），x∈R的值；
（Ⅱ）若数列{an}满足an=f（0）+f（$\frac{1}{n}$）+f（$\frac{2}{n}$）+…+f（$\frac{n-1}{n}$）+f（1）（n∈N*），求数列{an}的通项公式．
10．函数f（x）=ln（9-3x）的定义域是（　　）
A．[2，+∞）B．（2，+∞）C．（-∞，2]D．（-∞，2）
7．已知M（4，0），N（1，0），若动点P满足$\overrightarrow{MN}$•$\overrightarrow{MP}$=6|$\overrightarrow{NP}$|，求动点P的轨迹方程．
14．△ABC的内角A、B、C所对的边为a、b、c，则下列命题正确的是②③．
①若A＜B，则 cos2A＜cos2B       ②若ab＞c2，则C$＜\frac{π}{3}$
③若a+b＞2c，则 C$＜\frac{π}{3}$          ④若（a+b）c＜2ab，则C＞$\frac{π}{2}$．
4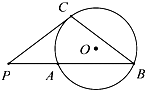．如图，PC是⊙O的切线，C为切点，PAB为割线，PC=2，PA=1，∠P=60°，则BC=（　　）
A．3B．2C．3$\sqrt{2}$D．2$\sqrt{3}$
11．在极坐标系中，已知A（$\sqrt{2}$，0）到直线l：ρsin（θ-$\frac{π}{4}$）=m，（m＞0）的距离为3．
（1）求m的值．
（2）设P是直线l上的动点，点Q在线段OP上，满足|$\overrightarrow{OP}$|•|$\overrightarrow{OQ}$|=1，求点Q的轨迹方程．
8．已知向量$\overrightarrow a=（-1，x，3），\overrightarrow b=（2，-4，y）$，且$\overrightarrow a∥\overrightarrow b$，那么x+y的值为-4．
9．若实数x，y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$，则函数z=2x+y的最大值为（　　）
A．12B．$\frac{32}{5}$C．3D．15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网