题目内容
5.设f(x)是定义在R上的增函数,且对于任意的x都有f(1-x)+f(1+x)=0恒成立,a,b满足不等式组$\left\{\begin{array}{l}{f({a}^{2}-6a+23)+f({b}^{2}-8b)≤0}\\{f(b+1)>f(5)}\end{array}\right.$,那么a2+b2的取值范围是( )| A. | (17,49] | B. | [9,49] | C. | (17,41] | D. | [9,41] |
分析 由f(1-x)+f(1+x)=0恒成立,可将不等式可化为f(a2-6a+23)≤f(2-b2+8b),利用f(x)的单调性,可化为关于m的整式不等式(a-3)2+(b-4)2≤4,分析(a-3)2+(b-4)2≤4的几何意义,即可求得a2+n2 的取值范围.
解答 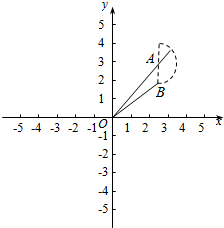 解:∵对于任意的x都有f(1-x)+f(1+x)=0恒成立
解:∵对于任意的x都有f(1-x)+f(1+x)=0恒成立
∴f(1-x)=-f(1+x)
∵f(a2-6a+23)+f(b2-8b)≤0,
∴f(a2-6a+23)≤-f[(1+(b2-8b-1)],
∴f(a2-6a+23)≤f[(1-(b2-8b-1)]=f(2-b2+8b),
∵f(x)是定义在R上的增函数,
∴a2-6a+23≤2-b2+8b,
∴(a-3)2+(b-4)2≤4(b>4)
∵(m-3)2+(n-4)2=4的圆心坐标为:(3,4),半径为2,
∴(m-3)2+(n-4)2=4(b>4)内的点到原点距离的取值范围为($\sqrt{{1}^{2}+{4}^{2}}$,5+2],即($\sqrt{17}$,7],
∵m2+n2 表示(m-3)2+(n-4)2=4内的点到原点距离的平方,
∴m2+n2 的取值范围是(17,49].
故选:A
点评 本题考查函数的奇偶性与单调性,考查不等式的含义,解题的关键是确定半圆内的点到原点距离的取值范围.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
20.函数f(x)=x2+(a-3)x+1在区间[-1,+∞)上是递增的,则实数a的取值范围是( )
| A. | [-3,0) | B. | (-∞,-3] | C. | [5,+∞) | D. | (0,5] |