题目内容
10.已知函数f(x)=2$\sqrt{2}cosxcos(x+\frac{π}{4})$.(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)已知tanα=$\frac{1}{2}$,求f(-α)的值.
分析 利用两角和与差的三角函数化简函数的解析式.
(Ⅰ)利用正弦函数的单调性,直接求解函数的单调减区间即可.
(Ⅱ)化简所求表达式为正切函数的形式,然后求解即可.
解答 (本题满分12分)
解:$f(x)=2\sqrt{2}cosxcos(x+\frac{π}{4})$=$2\sqrt{2}cosx(cosxcos\frac{π}{4}-sinxsin\frac{π}{4})$=2cos2x-2sinxcosx=cos2x-sin2x+1=$1-\sqrt{2}sin(2x-\frac{π}{4})$…(2分)
(Ⅰ)f(x)的单调递减区间即是$y=\sqrt{2}sin(2x-\frac{π}{4})$的单调递增区间,
由$2kπ-\frac{π}{2}≤2x-\frac{π}{4}≤2kπ+\frac{π}{2}$(k∈Z)得:$kπ-\frac{π}{8}≤x≤kπ+\frac{3π}{8}$(k∈Z),
即$[kπ-\frac{π}{8},kπ+\frac{3π}{8}]$(k∈Z)是f(x)的单调递减区间.…(6分)
(Ⅱ)∵$tanα=\frac{1}{2}$,
∴f(-α)=2cos2α+2sinαcosα=$\frac{{2{{cos}^2}α+2sinαcosα}}{{{{sin}^2}α+{{cos}^2}α}}$=$\frac{2+2tanα}{{1+{{tan}^2}α}}$=$\frac{3}{{1+\frac{1}{4}}}=\frac{12}{5}$…(12分)
点评 本题考查两角和与差的三角函数,三句话是的化简求值,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某公司对员工进行身体素质综合测试,测试成绩分为优秀、良好、合格三个等级,测试结果如表:(单位:人)
按优秀、良好、合格三个等级分层,从中抽取50人,其中成绩为优的有30人.
(1)求a的值;
(2)若用分层抽样的方法,在合格的同学中按男女抽取一个容量为5的样本,从中任选2人,记X为抽取女生的人数,求X的分布列及数学期望.
| 优秀 | 良好 | 合格 | |
| 男 | 180 | 70 | 20 |
| 女 | 120 | a | 30 |
(1)求a的值;
(2)若用分层抽样的方法,在合格的同学中按男女抽取一个容量为5的样本,从中任选2人,记X为抽取女生的人数,求X的分布列及数学期望.
5.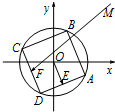 如图,已知圆O:x2+y2=4,M的坐标为(4,4),圆O的内接正方形ABCD的边AD,CD的中点分别为E,F,当正方形ABCD绕圆心O转动时,则$\overrightarrow{OE}•\overrightarrow{MF}$的取值范围是( )
如图,已知圆O:x2+y2=4,M的坐标为(4,4),圆O的内接正方形ABCD的边AD,CD的中点分别为E,F,当正方形ABCD绕圆心O转动时,则$\overrightarrow{OE}•\overrightarrow{MF}$的取值范围是( )
 如图,已知圆O:x2+y2=4,M的坐标为(4,4),圆O的内接正方形ABCD的边AD,CD的中点分别为E,F,当正方形ABCD绕圆心O转动时,则$\overrightarrow{OE}•\overrightarrow{MF}$的取值范围是( )
如图,已知圆O:x2+y2=4,M的坐标为(4,4),圆O的内接正方形ABCD的边AD,CD的中点分别为E,F,当正方形ABCD绕圆心O转动时,则$\overrightarrow{OE}•\overrightarrow{MF}$的取值范围是( )| A. | [-4,4] | B. | $[-4\sqrt{2},4\sqrt{2}]$ | C. | [-8,8] | D. | $[-8\sqrt{2},8\sqrt{2}]$ |
15. 图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
 图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩的茎叶图,图中第1次到14次的考试成绩依次记为A1,A2,…A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
2.设集合M={x|x2-2x-3<0},N=$\left\{{y|y=\sqrt{{x^2}+1},x∈R}\right\}$,则M∩N等于( )
| A. | (-1,1) | B. | [1,3) | C. | (0,1) | D. | (-1,0) |