题目内容
已知命题:平面直角坐标系xOy中,△ABC顶点A(-p,0)和C(p,0),顶点B在椭圆
+
=1(m>n>0,p=
)上,椭圆的离心率是e,则
=
,试将该命题类比到双曲线中,给出一个真命题:____________.
| x2 |
| m2 |
| y2 |
| n2 |
| m2-n2 |
| sinA+sinC |
| sinB |
| 1 |
| e |
∵根据椭圆的离心率的说法可以写出推理的前提,
平面直角坐标系xOy中,△ABC顶点A(-p,0)和C(p,0),
顶点B在双曲线
-
=1(m>0,n>0,p=
)上,
双曲线的离心率是e
后面的关于离心率的结果要计算出
∵
=
=
=
∴由正弦定理可以得到
=
,
故答案为:平面直角坐标系xOy中,△ABC顶点A(-p,0)和C(p,0),
顶点B在双曲线
-
=1(m>0,n>0,p=
)上,
双曲线的离心率是e,则
=
,
平面直角坐标系xOy中,△ABC顶点A(-p,0)和C(p,0),
顶点B在双曲线
| x2 |
| m2 |
| y2 |
| n2 |
| m2+n2 |
双曲线的离心率是e
后面的关于离心率的结果要计算出
∵
| 1 |
| e |
| a |
| c |
| 2a |
| 2c |
| |AB-BC| |
| AC |
∴由正弦定理可以得到
| 1 |
| e |
| |sinC-sinA| |
| sinB |
故答案为:平面直角坐标系xOy中,△ABC顶点A(-p,0)和C(p,0),
顶点B在双曲线
| x2 |
| m2 |
| y2 |
| n2 |
| m2+n2 |
双曲线的离心率是e,则
| 1 |
| e |
| |sinC-sinA| |
| sinB |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
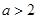 时,
时,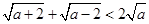
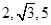 不可能是同一个等差数列中的三项
不可能是同一个等差数列中的三项

