题目内容
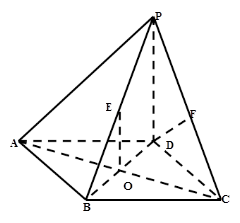
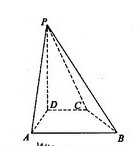
已知在四棱锥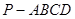 中,底面
中,底面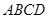 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱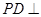 平面
平面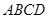 ,且
,且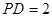 ,
, 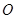 为底面对角线的交点,
为底面对角线的交点,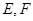 分别为棱
分别为棱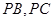 的中点
的中点
(1)求证: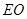 //平面
//平面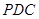 ;
;
(2)求证: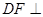 平面
平面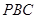 ;
;
(3)求点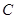 到平面
到平面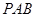 的距离。
的距离。
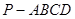 中,底面
中,底面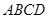 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱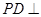 平面
平面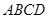 ,且
,且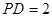 ,
, 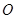 为底面对角线的交点,
为底面对角线的交点,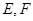 分别为棱
分别为棱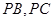 的中点
的中点
(1)求证:
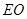 //平面
//平面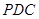 ;
;(2)求证:
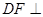 平面
平面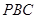 ;
;(3)求点
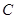 到平面
到平面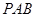 的距离。
的距离。(1)利用中位线性质定理可知 ,那么结合线面平行的判定定理的到。
,那么结合线面平行的判定定理的到。
(2)根据 面
面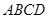
 ,又可知
,又可知 ,结合线面垂直的判定定理得到。
,结合线面垂直的判定定理得到。
(3)
 ,那么结合线面平行的判定定理的到。
,那么结合线面平行的判定定理的到。(2)根据
 面
面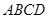
 ,又可知
,又可知 ,结合线面垂直的判定定理得到。
,结合线面垂直的判定定理得到。(3)

试题分析:(1)证明:
 是正方形,,
是正方形,, 为
为 的中点,又
的中点,又 为
为 的中点,
的中点, ,且
,且 平面
平面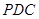 ,
, 平面
平面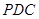 ,
, 平面
平面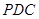 .
. (2)证明:
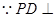 面
面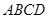 ,
, 面
面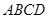 ,
, ,又可知
,又可知 ,而
,而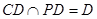 ,
, 面
面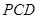 ,
, 面
面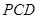 ,
, 面
面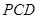 ,
, ,又
,又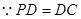 ,
, 为
为 的中点,
的中点,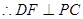 ,而
,而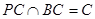 ,
,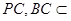 平面
平面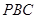 ,
, 平面
平面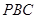
(3)解:设点
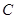 到平面
到平面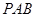 的距离为
的距离为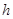 ,由(2)易证
,由(2)易证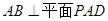 ,
, ,
,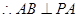 ,
, ,
,
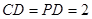
又
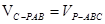 ,即
,即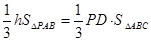 ,
, ,得
,得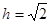
即点
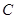 到平面
到平面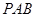 的距离为
的距离为
点评:主要是考查了空间中线面的平行,以及线面垂直的判定定理的运用,以及运用等体积法求解距离,属于中档题。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
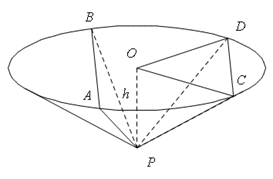
 .底面圆心为
.底面圆心为 ,其母线与底面所成的角为
,其母线与底面所成的角为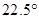 .
.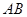 和
和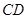 是底面圆
是底面圆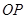 与平面
与平面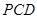 所成的角为
所成的角为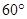 ,
, 
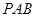 与平面
与平面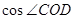 .
.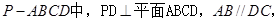
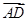 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥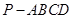 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);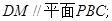
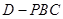 的体积.
的体积.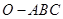 的侧棱
的侧棱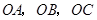 两两垂直,且
两两垂直,且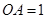 ,
,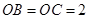 ,
,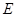 是
是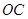 的中点.
的中点.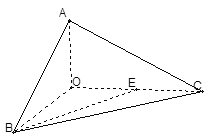
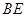 与
与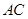 所成的角的余弦值
所成的角的余弦值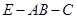 的余弦值
的余弦值 点到面
点到面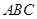 的距离
的距离 的棱长为1,
的棱长为1, 分别为线段
分别为线段 上的动点,则三棱锥
上的动点,则三棱锥 的体积为________.
的体积为________.
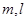 是不同的直线,
是不同的直线,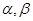 是不同的平面,给出下列五个命题:
是不同的平面,给出下列五个命题: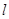 垂直于
垂直于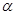 内的两条直线,则
内的两条直线,则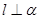 ;
;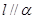 ,则
,则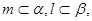 且
且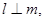 则
则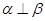 ;
;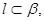 且
且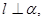 则
则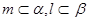 且
且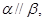 则
则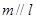 .其中正确命题的序号是
.其中正确命题的序号是