题目内容
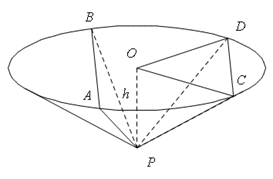
如图,圆锥顶点为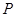 .底面圆心为
.底面圆心为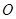 ,其母线与底面所成的角为
,其母线与底面所成的角为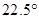 .
.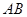 和
和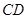 是底面圆
是底面圆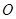 上的两条平行的弦,轴
上的两条平行的弦,轴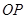 与平面
与平面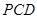 所成的角为
所成的角为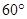 ,
,
(Ⅰ)证明:平面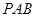 与平面
与平面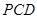 的交线平行于底面;
的交线平行于底面;
(Ⅱ)求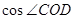 .
.
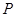 .底面圆心为
.底面圆心为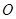 ,其母线与底面所成的角为
,其母线与底面所成的角为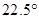 .
.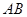 和
和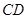 是底面圆
是底面圆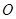 上的两条平行的弦,轴
上的两条平行的弦,轴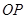 与平面
与平面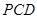 所成的角为
所成的角为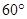 ,
, 
(Ⅰ)证明:平面
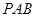 与平面
与平面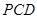 的交线平行于底面;
的交线平行于底面;(Ⅱ)求
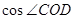 .
.(Ⅰ)见解析
(Ⅱ)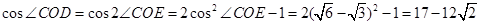
(Ⅱ)
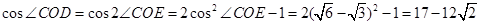
由公理可知,两面相交必交于一条直线,设面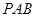 与面
与面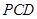 的交线为
的交线为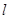
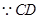 ∥
∥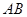
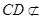 面
面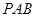 ,而
,而 面
面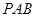
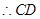 ∥面
∥面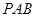
而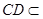 面
面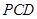
面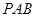
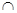 面
面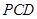 =
=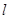
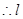 ∥
∥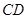
而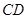
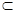 底面
底面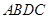
所以,平面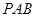 与平面
与平面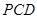 的交线平行于底面
的交线平行于底面
(2)
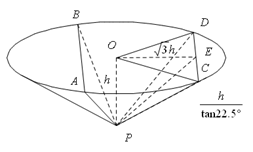
取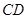 的中点
的中点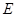 ,连接
,连接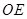 ,
,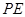 ,则
,则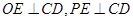
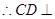 面
面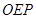 ,
,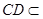 底面
底面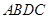
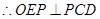
所以直线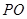 在面
在面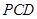 上的射影为
上的射影为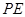
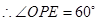
设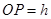 ,则
,则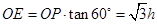
由题意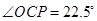
则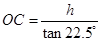
而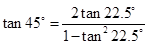 ,
,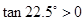 ,解得
,解得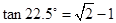
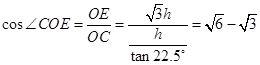
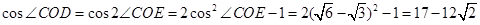
本题一反常态,考查旋转体的特征,考生一时有点迷惑,但只要静下心来,这道题其实不难.第(1)题,考生要知道两面相交必交于一条直线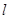 ,接着只需根据线线平行证明线面平行,而线线平行又要通过线面平行来证明,理顺这个关系,这道题就可以准确的证出了,通过这道题提醒考生课本上一些证明的定理和性质要熟练掌握.第(2)题,考生先要找出母线与底面所成的角是
,接着只需根据线线平行证明线面平行,而线线平行又要通过线面平行来证明,理顺这个关系,这道题就可以准确的证出了,通过这道题提醒考生课本上一些证明的定理和性质要熟练掌握.第(2)题,考生先要找出母线与底面所成的角是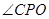 ,设
,设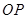 的长度表示出
的长度表示出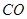 ,接着要能找出
,接着要能找出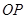 与平面
与平面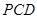 所成的角,利用这个角度求出
所成的角,利用这个角度求出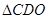 高的长度,再利用三角函数二倍角公式,三角形中的位置关系最终求出
高的长度,再利用三角函数二倍角公式,三角形中的位置关系最终求出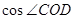 的值.
的值.
【考点定位】考查空间直线与直线,直线与平面,平面与平面的位置关系,线面垂直,面面垂直,直线与面所成的角等知识.
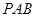 与面
与面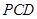 的交线为
的交线为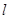
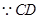 ∥
∥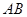
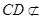 面
面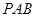 ,而
,而 面
面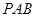
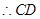 ∥面
∥面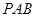
而
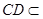 面
面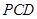
面
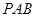
 面
面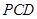 =
=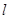
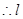 ∥
∥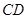
而
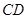
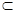 底面
底面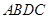
所以,平面
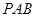 与平面
与平面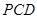 的交线平行于底面
的交线平行于底面(2)

取
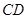 的中点
的中点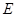 ,连接
,连接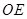 ,
,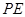 ,则
,则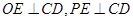
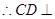 面
面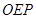 ,
,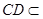 底面
底面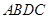
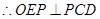
所以直线
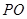 在面
在面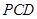 上的射影为
上的射影为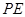
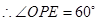
设
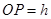 ,则
,则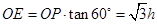
由题意
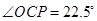
则
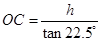
而
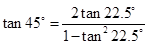 ,
,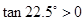 ,解得
,解得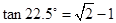
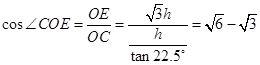
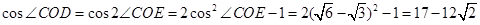
本题一反常态,考查旋转体的特征,考生一时有点迷惑,但只要静下心来,这道题其实不难.第(1)题,考生要知道两面相交必交于一条直线
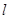 ,接着只需根据线线平行证明线面平行,而线线平行又要通过线面平行来证明,理顺这个关系,这道题就可以准确的证出了,通过这道题提醒考生课本上一些证明的定理和性质要熟练掌握.第(2)题,考生先要找出母线与底面所成的角是
,接着只需根据线线平行证明线面平行,而线线平行又要通过线面平行来证明,理顺这个关系,这道题就可以准确的证出了,通过这道题提醒考生课本上一些证明的定理和性质要熟练掌握.第(2)题,考生先要找出母线与底面所成的角是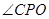 ,设
,设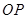 的长度表示出
的长度表示出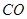 ,接着要能找出
,接着要能找出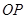 与平面
与平面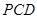 所成的角,利用这个角度求出
所成的角,利用这个角度求出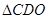 高的长度,再利用三角函数二倍角公式,三角形中的位置关系最终求出
高的长度,再利用三角函数二倍角公式,三角形中的位置关系最终求出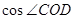 的值.
的值.【考点定位】考查空间直线与直线,直线与平面,平面与平面的位置关系,线面垂直,面面垂直,直线与面所成的角等知识.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
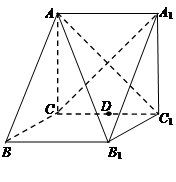
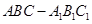 中,侧棱
中,侧棱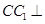 底面
底面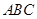 ,
,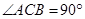 ,
,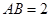 ,
,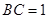 ,
,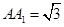 .
.
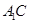
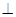 平面
平面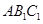 ;
;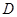 是棱
是棱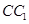 的中点,在棱
的中点,在棱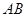 上是否存在一点
上是否存在一点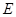 ,使
,使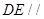 平面
平面 中,
中,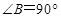 ,
,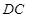 ∥
∥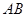 ,
,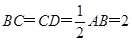 ,
, 为线段
为线段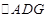 沿
沿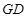 折起,使平面
折起,使平面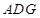 ⊥平面
⊥平面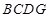 ,得到几何体
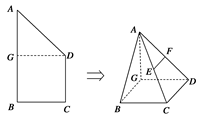
,得到几何体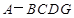 .
.
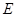 ,
,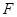 分别为线段
分别为线段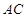 ,
,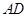 的中点,求证:
的中点,求证: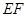 ∥平面
∥平面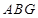 ;
;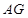 ⊥平面
⊥平面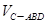 的值.
的值.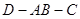 ,如图二,在二面角
,如图二,在二面角
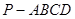 中,底面
中,底面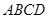 是边长为2的正方形,侧棱
是边长为2的正方形,侧棱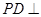 平面
平面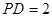 ,
, 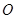 为底面对角线的交点,
为底面对角线的交点,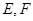 分别为棱
分别为棱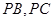 的中点
的中点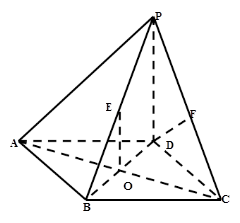
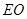 //平面
//平面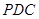 ;
;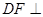 平面
平面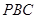 ;
;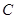 到平面
到平面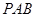 的距离。
的距离。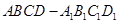 的棱长为1,
的棱长为1,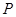 为
为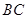 的中点,
的中点,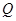 为线段
为线段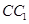 上的动点,过点
上的动点,过点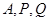 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为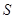 ,则下列命题正确的是 (写出所有正确命题的编号)。
,则下列命题正确的是 (写出所有正确命题的编号)。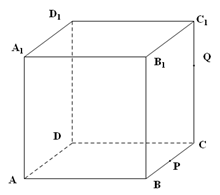
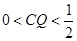 时,
时,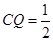 时,
时,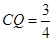 时,
时,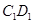 的交点
的交点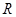 满足
满足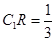
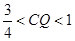 时,
时,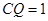 时,
时,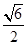
 ,
, ,
, ,则
,则 与
与 的位置关系是( )
的位置关系是( )

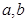 是两条不同的直线,
是两条不同的直线,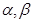 是两个不同的平面,则下列四个命题中,正确命题的个数是( )
是两个不同的平面,则下列四个命题中,正确命题的个数是( )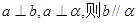 ②若
②若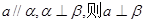
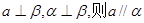 ④若
④若