题目内容
【题目】已知椭圆Γ:![]() 的左,右焦点分别为F1(
的左,右焦点分别为F1(![]() ,0),F2(
,0),F2(![]() ,0),椭圆的左,右顶点分别为A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k1,k2,满足
,0),椭圆的左,右顶点分别为A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k1,k2,满足![]() .
.
(1)求椭圆Γ的标准方程;
(2)若过椭圆Γ左顶点A作两条互相垂直的直线AM和AN,分别交椭圆Γ于M,N两点,问x轴上是否存在一定点Q,使得∠MQA=∠NQA成立,若存在,则求出该定点Q,否则说明理由.
【答案】(1)![]() (2)存在;定点
(2)存在;定点![]()
【解析】
(1)设![]() ,根据题意可得
,根据题意可得![]() ,结合椭圆的方程化简可得
,结合椭圆的方程化简可得![]() ,再由
,再由![]() 即可求解.
即可求解.
(2)根据设直线![]() 和
和![]() 的方程分别为
的方程分别为![]() 和
和![]() ,将直线方程与椭圆方程联立求出
,将直线方程与椭圆方程联立求出![]() 、
、![]() ,设
,设![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() 成立,则
成立,则![]() ,利用两点求斜率化简即可求得.
,利用两点求斜率化简即可求得.
解:(1)设![]() ,
,![]()
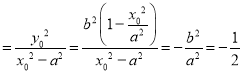 ,
,![]() ,
,
则![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)可知左顶点![]() ,且过点
,且过点![]() 的直线
的直线![]() 和
和![]() 的斜率存在,
的斜率存在,
设直线![]() 和
和![]() 的方程分别为
的方程分别为![]() 和
和![]() ,
,
设![]() ,
,
联立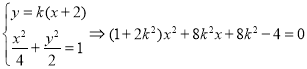 ,
,
![]() 直线
直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,
两点,
![]() ,
,
![]() ,
,![]()
同理![]() .
.
设![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() 成立,则
成立,则![]() ,
,
![]() ,则
,则![]()
![]() ,
,
![]() ,
,
即![]() ,解得
,解得![]() .
.
因此![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() 成立.
成立.

练习册系列答案
相关题目