题目内容

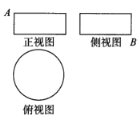
【题目】某圆柱的高为2，底面周长为16，则其体积为_________，若该圆柱的三视图如图所示，圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在侧视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为___________.

【答案】

【解析】

根据圆柱的底面周长为16，求得圆柱的底面半径，再结合高，利用柱体的体积公式求解，通过三视图可得点M，N在长为圆柱的高，宽为圆柱底面周长的的矩形对角线的端点上，利用勾股定理求解.

因为圆柱的底面周长为16，

所以圆柱的底面半径为，

所以圆柱的体积为.

由三视图得点M，N在长为圆柱的高，宽为圆柱底面周长的的矩形对角线的端点上，

如图所示：

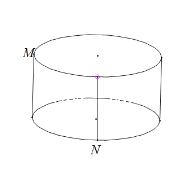
则最短路径为.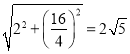

故答案为：①；②

练习册系列答案
相关题目

【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额（单位：万元）进行统计并得到如图折线图.

下面关于两个门店营业额的分析中，错误的是( )

A.甲门店的营业额折线图具有较好的对称性，故而营业额的平均值约为32万元

B.根据甲门店的营业额折线图可知，该门店营业额的平均值在[20，25]内

C.根据乙门店的营业额折线图可知，其营业额总体是上升趋势

D.乙门店在这9个月份中的营业额的极差为25万元

【题目】已知抛物线的顶点是椭圆的中心，焦点与该椭圆的右焦点重合.

（1）求抛物线的方程；

（2）已知动直线过点，交抛物线于，两点，坐标原点为的中点，求证；

（3）在（2）的条件下，是否存在垂直于轴的直线被以为直径的圆所截得的弦长恒为定值？如果存在，求出的方程；如果不存在，请说明理由.

【题目】如图，已知多面体中，平面，，三角形是等边三角形，且，为的中点．

（Ⅰ）求证：平面；

（Ⅱ）求直线与平面所成角的正弦值．

【题目】在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球，分别标有数字1，2，3，4.现每次有放回地从中任意取出一个小球，直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第3次停止摸球的概率，利用计算机软件产生随机数，每1组中有3个数字，分别表示每次摸球的结果，经随机模拟产生了以下18组随机数：

131 432 123 233 234 122 332 141 312 241 122 214 431 241 141 433 223 442

由此可以估计恰好在第3次停止摸球的概率为（ ）

A.B.C.D.

【题目】椭圆C：的离心率为，其右焦点到椭圆C外一点的距离为，不过原点O的直线l与椭圆C相交于A，B两点，且线段AB的长度为2．

1求椭圆C的方程；

2求面积S的最大值．

【题目】已知抛物线焦点为，且，，过作斜率为的直线交抛物线于、两点.

（1）若，，求；

（2）若为坐标原点，为定值，当变化时，始终有，求定值的大小；

（3）若，，，当改变时，求三角形的面积的最大值.

【题目】已知椭圆Γ：的左，右焦点分别为F1(，0)，F2(，0)，椭圆的左，右顶点分别为A，B，已知椭圆Γ上一异于A，B的点P，PA，PB的斜率分别为k1，k2，满足.

（1）求椭圆Γ的标准方程；

（2）若过椭圆Γ左顶点A作两条互相垂直的直线AM和AN，分别交椭圆Γ于M，N两点，问x轴上是否存在一定点Q，使得∠MQA=∠NQA成立，若存在，则求出该定点Q，否则说明理由.

【题目】“众志成城，抗击疫情，一方有难，八方支援”，在此次抗击疫情过程中，各省市都派出援鄂医疗队. 假设汕头市选派名主任医生，名护士，组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援，每个小组包括名主任医生和名护士，则不同的分配方案有（ ）

A.种B.种C.种D.种

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网