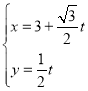题目内容
【题目】如图,已知直三棱柱ABC﹣A1B1C1,E,F分别是棱CC1,AB的中点.

(1)证明:CF∥平面AEB1.
(2)若AC=BC=AA1=4,∠ACB=90°,求三棱锥B1﹣ECF的体积.
【答案】(1)证明见解析(2)![]() .
.
【解析】
(1)取AB1的中点G,连结EG,FG,推导出四边形FGEC是平行四边形,从而CF∥EG,由此能证明CF∥平面AEB1.
(2)求出△B1EC的面积,三棱锥F﹣B1CE的高为![]() 2,由此能求出三棱锥F﹣B1CE的体积,再利用等体积法求解.
2,由此能求出三棱锥F﹣B1CE的体积,再利用等体积法求解.
(1)如图所示:

取AB1的中点G,连结EG,FG,
∵F,G分别是AB,AB1的中点,
∴FG∥EC,FG=EC,
∴四边形FGEC是平行四边形,
∴CF∥EG,
∵CF平面AEB1,EG平面AEB1,
∴CF∥平面AEB1.
(2)在直三棱柱ABC﹣A1B1C1中,
∵BC=AA1=4,E是CC1的中点,
∴△B1EC的面积为![]() ,
,
∵AC⊥BC,平面ABC![]() 平面
平面![]() ,平面ABC
,平面ABC![]() 平面
平面![]() =BC,
=BC,
∴AC![]() 平面
平面![]() ,
,
∵F是AB的中点,
∴三棱锥F﹣B1CE的高为![]() 2,
2,
∴三棱锥F﹣B1CE的体积为V![]() .
.
∵三棱锥B1﹣ECF的体积与三棱锥F﹣B1CE的体积相等,
∴三棱锥B1﹣ECF的体积为![]() .
.

练习册系列答案
相关题目