题目内容
设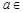 R,函数
R,函数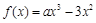 .
.
(1)若x=2是函数y=f(x)的极值点,求实数a的值;
(2)若函数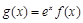 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围.
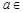 R,函数
R,函数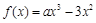 .
.(1)若x=2是函数y=f(x)的极值点,求实数a的值;
(2)若函数
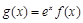 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:解题思路:(1)求导数,利用
 求解即可;(2)求导数,利用
求解即可;(2)求导数,利用 在
在 上是减函数的充要条件是
上是减函数的充要条件是 在
在 上恒成立.规律总结:利用导数研究函数的性质是常见题型,主要是通过导数研究函数的单调性、求单调区间、求极值、最值以及不等式恒成立等问题,往往计算量较大,思维量大,要求学生有较高的逻辑推理能力.
上恒成立.规律总结:利用导数研究函数的性质是常见题型,主要是通过导数研究函数的单调性、求单调区间、求极值、最值以及不等式恒成立等问题,往往计算量较大,思维量大,要求学生有较高的逻辑推理能力.试题解析:(1)由
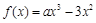 ,得
,得 ,
,因为x=2是函数y=f(x)的极值点,所以
 ,解得
,解得 ,
,经检验,x=2是函数y=f(x)的极小值点,所以
 .
.(2)由
 ,得
,得 ,
,因为
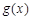 在区间[0,2]上是减函数,
在区间[0,2]上是减函数,所以
 在区间[0,2]上恒成立,
在区间[0,2]上恒成立,只需
 在区间(0,2]上恒成立即可,
在区间(0,2]上恒成立即可,即
 ,只需要
,只需要 在(0,2]上恒成立,
在(0,2]上恒成立,令
 ,则
,则 恒成立,
恒成立,所以函数
 在区间(0,2]上单调递减,
在区间(0,2]上单调递减,所以
 的最小值
的最小值 ,故
,故 ,
,所以实数a的取值范围是
 .
.
练习册系列答案
相关题目
 .
.
 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.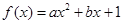 (
(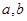 为实数,
为实数,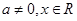 ),
),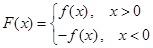 ,⑴若
,⑴若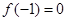 ,且函数
,且函数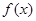 的值域为
的值域为 ,求
,求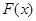 的表达式;
的表达式;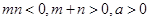 ,且函数
,且函数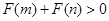 是否大0?
是否大0?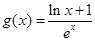 ,当
,当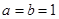 时,证明:对任意实数
时,证明:对任意实数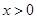 ,
,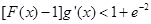 (其中
(其中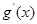 是
是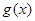 的导函数) .
的导函数) .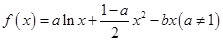 ,曲线
,曲线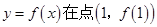 处的切线斜率为0
处的切线斜率为0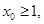 使得
使得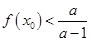 ,求a的取值范围。
,求a的取值范围。 时,每小时消耗的煤价值
时,每小时消耗的煤价值 元,至于其他费用每小时要
元,至于其他费用每小时要 元,问火车行驶的速度为多少时,才能使火车从甲城开往乙城的总费用最省?
元,问火车行驶的速度为多少时,才能使火车从甲城开往乙城的总费用最省? 有两个极值点
有两个极值点 ,且
,且
 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;


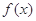 定义在
定义在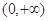 上的非负可导函数,且满足
上的非负可导函数,且满足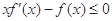 ,对任意正数
,对任意正数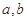 , 若
, 若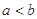 ,则必有( ).
,则必有( ).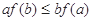



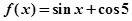 ,则该函数在点
,则该函数在点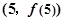 处切线的斜率等于( )
处切线的斜率等于( )



 ;③(ex)′=ex;④(
;③(ex)′=ex;④( )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.