题目内容
设函数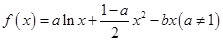 ,曲线
,曲线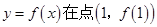 处的切线斜率为0
处的切线斜率为0
求b;若存在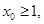 使得
使得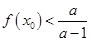 ,求a的取值范围。
,求a的取值范围。
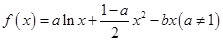 ,曲线
,曲线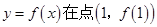 处的切线斜率为0
处的切线斜率为0求b;若存在
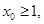 使得
使得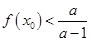 ,求a的取值范围。
,求a的取值范围。(1)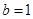 ;(2)
;(2)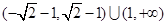 .
.
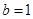 ;(2)
;(2)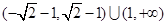 .
.试题分析:(1)根据曲线在某点处的切线与此点的横坐标的导数的对应关系,可先对函数进行求导可得:
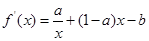 ,利用上述关系不难求得
,利用上述关系不难求得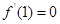 ,即可得
,即可得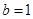 ;(2)由第(1)小题中所求b,则函数
;(2)由第(1)小题中所求b,则函数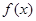 完全确定下来,则它的导数可求出并化简得:
完全确定下来,则它的导数可求出并化简得: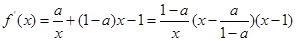 根据题意可得要对
根据题意可得要对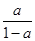 与
与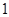 的大小关系进行分类讨论,则可分以下三类:(ⅰ)若
的大小关系进行分类讨论,则可分以下三类:(ⅰ)若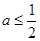 ,则
,则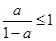 ,故当
,故当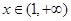 时,
时,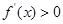 ,
,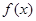 在
在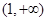 单调递增,所以,存在
单调递增,所以,存在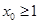 ,使得
,使得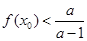 的充要条件为
的充要条件为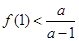 ,即
,即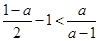 ,所以
,所以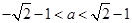 .(ⅱ)若
.(ⅱ)若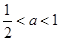 ,则
,则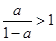 ,故当
,故当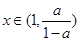 时,
时,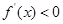 ;当
;当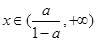 时,
时,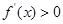 ,
,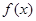 在
在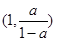 单调递减,在
单调递减,在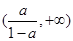 单调递增.所以,存在
单调递增.所以,存在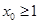 ,使得
,使得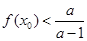 的充要条件为
的充要条件为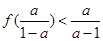 ,无解则不合题意.(ⅲ)若
,无解则不合题意.(ⅲ)若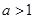 ,则
,则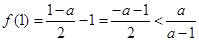 .综上,a的取值范围是
.综上,a的取值范围是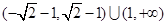 .
.试题解析:(1)
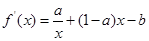 ,
,由题设知
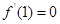 ,解得
,解得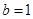 .
.(2)
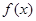 的定义域为
的定义域为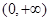 ,由(1)知,
,由(1)知,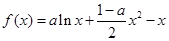 ,
,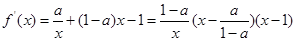
(ⅰ)若
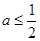 ,则
,则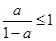 ,故当
,故当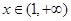 时,
时,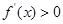 ,
,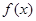 在
在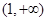 单调递增,
单调递增,所以,存在
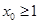 ,使得
,使得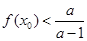 的充要条件为
的充要条件为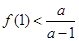 ,即
,即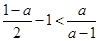 ,
,所以
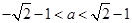 .
.(ⅱ)若
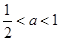 ,则
,则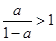 ,故当
,故当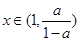 时,
时,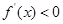 ;
;当
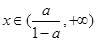 时,
时,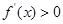 ,
,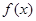 在
在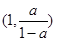 单调递减,在
单调递减,在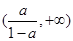 单调递增.
单调递增.所以,存在
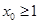 ,使得
,使得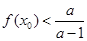 的充要条件为
的充要条件为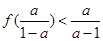 ,
,而
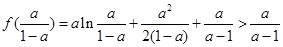 ,所以不合题意.
,所以不合题意.(ⅲ)若
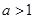 ,则
,则 .
.综上,a的取值范围是
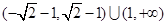 .
.
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
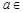 R,函数
R,函数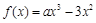 .
.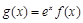 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围.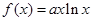
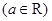 ,已知曲线
,已知曲线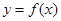 在点
在点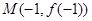 处的切线方程是
处的切线方程是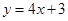 .
.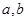 的值;并求出函数的单调区间;
的值;并求出函数的单调区间;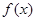 在区间
在区间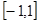 上的最值.
上的最值.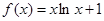
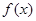 在
在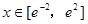 上的最大值与最小值;
上的最大值与最小值;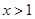 时,函数
时,函数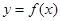 的图像恒在直线
的图像恒在直线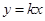 上方,求实数
上方,求实数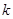 的取值范围;
的取值范围;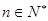 时,
时,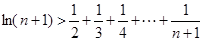
 ,设
,设 为
为 的导数,
的导数,
 的值;
的值; 都成立.
都成立. ,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )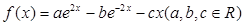 的导函数
的导函数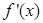 为偶函数,且曲线
为偶函数,且曲线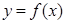 在点
在点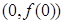 处的切线的斜率为
处的切线的斜率为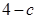 .
.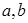 的值;
的值; 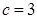 ,判断
,判断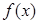 的单调性;
的单调性;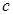 的取值范围.
的取值范围.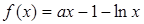
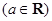 .
.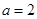 时,求函数
时,求函数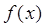 的单调区间;
的单调区间;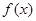 在
在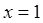 处取得极值,对
处取得极值,对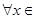
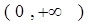 ,
,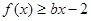 恒成立,求实数
恒成立,求实数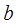 的取值范围;
的取值范围;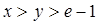 时,求证:
时,求证: .
.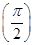 +f2
+f2