题目内容
18．若向量$\overrightarrow{AB}$=（-2，-3），$\overrightarrow{AC}$=（-4，-7），则$\overrightarrow{BC}$=（ ）| A． | （-2，-4） | B． | （2，4） | C． | （6，10） | D． | （-6，-10） |
分析 由$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$，即可得出结论．
解答 解：向量$\overrightarrow{AB}$=（-2，-3），$\overrightarrow{AC}$=（-4，-7），则$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=（-2，-4），
故选：A．
点评 本题考查了向量的减法运算，深刻理解向量的减法运算法则是解决问题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
9．
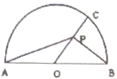如图，AB=2，O为圆心，C为半圆上不同于A，B的任意一点，若P为半径OC上的动点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$的最小值等于（ ）
如图，AB=2，O为圆心，C为半圆上不同于A，B的任意一点，若P为半径OC上的动点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$）•$\overrightarrow{PC}$的最小值等于（ ）| A． | -$\frac{1}{2}$ | B． | -2 | C． | -1 | D． | -$\frac{1}{4}$ |
6．已知tanα=4，则$\frac{{1+cos2α+8{{sin}^2}α}}{sin2α}$的值为（ ）
| A． | 18 | B． | $\frac{1}{4}$ | C． | 16 | D． | $\frac{65}{4}$ |