题目内容
已知函数f(x)=x2013+ax3-
-8,f(-2)=10,则f(2)=______.
| b |
| x |
令g(x)=x2013+ax3-
.
该函数的定义域为{x|x≠0}.
由g(-x)=(-x)2013+a(-x)3-
=-(x2013+ax3-
)=-g(x).
∴函数g(x)为定义域内的奇函数.
∵f(-2)=g(-2)-8=10,∴g(-2)=18,g(2)=-18.
则f(2)=g(2)-8=-18-8=-26.
故答案为:-26.
| b |
| x |
该函数的定义域为{x|x≠0}.
由g(-x)=(-x)2013+a(-x)3-
| b |
| -x |
| b |
| x |
∴函数g(x)为定义域内的奇函数.
∵f(-2)=g(-2)-8=10,∴g(-2)=18,g(2)=-18.
则f(2)=g(2)-8=-18-8=-26.
故答案为:-26.

练习册系列答案
相关题目
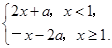
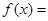
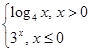 ,则
,则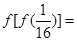 ( )
( )