题目内容
11.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|=4,($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,若对每一个确定的$\overrightarrow b$,|$\overrightarrow{c}$|的最大值和最小值分别为m,n,则m-n的值为( )| A. | 随$|\overrightarrow a|$增大而增大 | B. | 随$|\overrightarrow a|$增大而减小 | C. | 是2 | D. | 是4 |
分析 通过假设$\overrightarrow{a}$=(4,0)、$\overrightarrow{b}$=(2,2$\sqrt{3}$)、$\overrightarrow{c}$=(x,y),利用($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,计算可得向量$\overrightarrow{c}$的终点在以(3,$\sqrt{3}$)为圆心、半径等于2的圆上,进而可得结论.
解答 解:假设$\overrightarrow{a}$=(4,0)、$\overrightarrow{b}$=(2,2$\sqrt{3}$)、$\overrightarrow{c}$=(x,y),
∵($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,
∴(4-x,-y)•(2-x,2$\sqrt{3}$-y)=x2+y2-6x-2$\sqrt{3}$y+8=0,
即(x-3)2+(y-$\sqrt{3}$)2=4,
∴满足条件的向量$\overrightarrow{c}$的终点在以(3,$\sqrt{3}$)为圆心、半径等于2的圆上,
∴|$\overrightarrow{c}$|的最大值与最小值分别为m=2+2$\sqrt{3}$,n=2$\sqrt{3}$-2,
∴m-n=4,
故选:D.
点评 本题主要考查两个向量的数量积的运算,利用特殊值代入法,是一种简单有效的方法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
16.如图是函数y=2sin(ωx+ϕ)(ω>0)图象的一部分,则ω和ϕ为( )


| A. | ω=$\frac{11}{5}$,ϕ=-$\frac{5π}{6}$ | B. | ω=$\frac{7}{5}$,ϕ=-$\frac{π}{6}$ | C. | ω=$\frac{17}{5}$,ϕ=-$\frac{5π}{6}$ | D. | ω=$\frac{13}{5}$,ϕ=-$\frac{π}{6}$ |
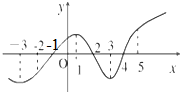 已知函数y=f(x)的导函数f′(x)的图象如图所示,则函数f(x)在区间[-3,5]上取得极大值时,x的取值为2.
已知函数y=f(x)的导函数f′(x)的图象如图所示,则函数f(x)在区间[-3,5]上取得极大值时,x的取值为2.