题目内容
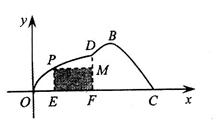
如图,某市准备在一个湖泊的一侧修建一条直路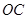 ,另一侧修建一条观光大道,它的前一段
,另一侧修建一条观光大道,它的前一段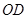 是以
是以 为顶点,
为顶点,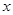 轴为对称轴,开口向右的抛物线的一部分,后一段
轴为对称轴,开口向右的抛物线的一部分,后一段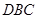 是函数
是函数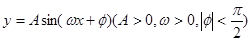 ,
,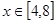 时的图象,图象的最高点为
时的图象,图象的最高点为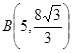 ,
,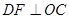 ,垂足为
,垂足为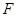 .
.
(1)求函数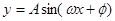 的解析式;
的解析式;
(2)若在湖泊内修建如图所示的矩形水上乐园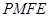 ,问:点
,问:点 落在曲线
落在曲线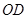 上何处时,水上乐园的面积最大?
上何处时,水上乐园的面积最大?
(1) ;(2)点
;(2)点 的坐标为
的坐标为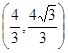 时
时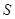 最大.
最大.
解析试题分析:(1)利用图像分析得出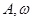 ,代入点后求出
,代入点后求出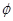 ,从而得出解析式;(2)先构建函数模型
,从而得出解析式;(2)先构建函数模型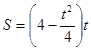 ,
,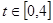 ,然后利用函数的导数求出最值和点P的位置.
,然后利用函数的导数求出最值和点P的位置.
试题解析:(1)对于函数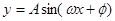 ,由图象知:
,由图象知: .将
.将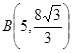 代入到
代入到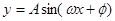 中,
中,
得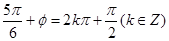 ,又
,又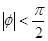 ,所以
,所以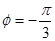 . 4分
. 4分
故 5分
5分
(2)在 中,令
中,令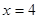 ,得
,得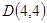 ,
,
所以曲线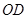 所在抛物线的方程为
所在抛物线的方程为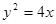 7分
7分
设点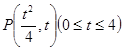 , 则矩形
, 则矩形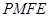 的面积为
的面积为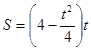 ,
,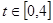 .
.
因为 ,由
,由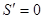 ,得
,得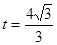 9分
9分
且当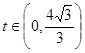 时,
时,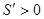 ,则
,则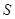 单调递增,
单调递增,
当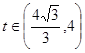 时,
时,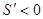 ,则
,则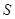 单调递减 11分
单调递减 11分
所以当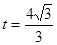 时,
时,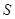 最大,此时点
最大,此时点 的坐标为
的坐标为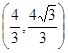 13分
13分
(若没考虑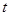 的范围,则扣2分)
的范围,则扣2分)
考点:1.利用图像求函数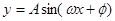 的解析式;2.函数模型的应用
的解析式;2.函数模型的应用

练习册系列答案
相关题目
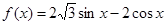
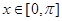 ,求
,求 的最大值和最小值;
的最大值和最小值;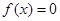 ,求
,求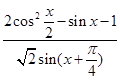 的值.
的值.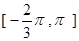 上的函数
上的函数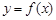 的图象关于直线
的图象关于直线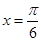 对称,当
对称,当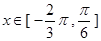 时函数
时函数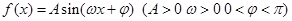 图象如图所示.
图象如图所示. 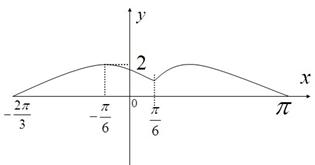
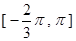 的表达式;
的表达式;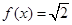 的解;
的解; 的值,使得
的值,使得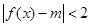 在
在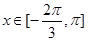 上恒成立;若存在,求出
上恒成立;若存在,求出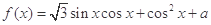 .
.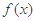 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;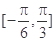 上的最大值与最小值的和为
上的最大值与最小值的和为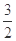 ,求
,求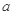 的值.
的值. 中,已知内角
中,已知内角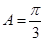 ,边
,边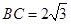 .设内角
.设内角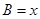 ,
, .
.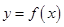 的解析式和定义域;
的解析式和定义域; ,
, ,且
,且 ,其中A、B、C是
,其中A、B、C是 ABC的内角,
ABC的内角, 分别是角A,B,C的对边。
分别是角A,B,C的对边。 的取值范围;
的取值范围;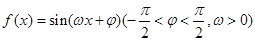 的最小正周期为
的最小正周期为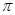 ,其图像经过点
,其图像经过点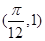
 的解析式;
的解析式;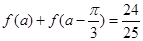 且
且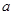 为锐角,求
为锐角,求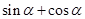 的值.
的值.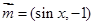 ,向量
,向量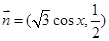 ,函数
,函数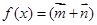 ·
·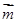 .
. 的最小正周期T;
的最小正周期T;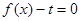 在
在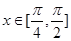 上有解,求实数
上有解,求实数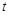 的取值范围.
的取值范围.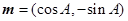 ,
,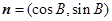 ,
,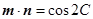 ,其中
,其中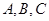 为
为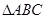 的内角.
的内角.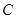 的大小;
的大小;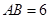 ,且
,且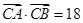 ,求
,求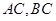 的长.
的长.