题目内容
19.己知f(x)为奇函数,g(x)为偶函数,且f(x)+g(x)=21og2(1-x).(1)求函数f(x)及g(x)的解析式;
(2)用函数单调性的定义证明:函数g(x)在(0,1)上是减函数;
(3)若关于x的方程f(2x)=m有解,求实数m的取值范围.
分析 (1)根据f(x),g(x)的奇偶性便有-f(x)+g(x)=2log2(1+x),联立f(x)+g(x)=2log2(1-x)便可解出f(x)=$lo{g}_{2}\frac{1-x}{1+x}$,g(x)=$lo{g}_{2}(1-{x}^{2})$;
(2)根据减函数的定义,设任意的x1,x2∈(0,1),且x1<x2,然后作差,可以得出$1-{{x}_{1}}^{2}>1-{{x}_{2}}^{2}$,根据对数函数的单调性便可得出g(x1)>g(x2),从而得出g(x)在(0,1)上单调递减;
(3)求出$f({2}^{x})=lo{g}_{2}(-1+\frac{2}{1+{2}^{x}})$,根据1-2x>0便可得出1+2x的范围,从而得出-1+$\frac{2}{1+{2}^{x}}$的范围,根据对数函数的单调性便可得出f(2x)的范围,从而便可得出m的取值范围.
解答 解:(1)根据题意:f(-x)+g(-x)=2log2(1+x);
∴-f(x)+g(x)=2log2(1+x),联立f(x)+g(x)=2log2(1-x)得:
f(x)=log2(1-x)-log2(1+x)=$lo{g}_{2}\frac{1-x}{1+x}$,g(x)=log2(1+x)+log2(1-x)=$lo{g}_{2}(1-{x}^{2})$;
即$f(x)=lo{g}_{2}\frac{1-x}{1+x},g(x)=lo{g}_{2}(1-{x}^{2})$;
(2)设x1,x2∈(0,1),且x1<x2,则:
$g({x}_{1})-g({x}_{2})=lo{g}_{2}(1-{{x}_{1}}^{2})-lo{g}_{2}(1-{{x}_{2}}^{2})$;
∵0<x1<x2<1;
∴${{x}_{1}}^{2}<{{x}_{2}}^{2}$;
∴$1-{{x}_{1}}^{2}>1-{{x}_{2}}^{2}$;
∴$lo{g}_{2}(1-{{x}_{1}}^{2})>lo{g}_{2}(1-{{x}_{2}}^{2})$;
∴g(x1)>g(x2);
∴g(x)在(0,1)上是减函数;
(3)$f({2}^{x})=lo{g}_{2}\frac{1-{2}^{x}}{1+{2}^{x}}=lo{g}_{2}(-1+\frac{2}{1+{2}^{x}})$;
∵1-2x>0;
∴0<2x<1;
∴$\frac{1}{2}<\frac{1}{1+{2}^{x}}<1$;
∴$0<-1+\frac{2}{1+{2}^{x}}<1$;
∴f(2x)<0;
∴m<0;
∴m的取值范围为(-∞,0).
点评 考查奇函数、偶函数的定义,对数的运算,以及减函数的定义,根据减函数的定义证明一个函数为减函数的方法和过程,作差的方法比较g(x1),g(x2),对数函数的单调性,分离常数法的运用.

| A. | 三棱柱 | B. | 三棱台 | C. | 三棱锥 | D. | 四棱锥 |
| A. | r1,r2,r3成等差数列 | B. | $\frac{1}{{r}_{1}}$+$\frac{1}{{r}_{2}}$=$\frac{2}{{r}_{3}}$ | ||
| C. | r1,r2,r3成等比数列 | D. | 以上结论全不对 |
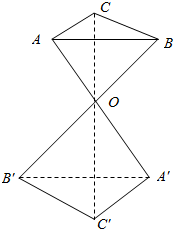 如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.
如图,△ABC和△A′B′C′的对应顶点的连线AA′,BB′,CC′交于同一点O,且$\frac{AO}{OA′}=\frac{BO}{OB′}=\frac{CO}{OC′}=\frac{2}{3}$.