��Ŀ����
����Ŀ��һ����ѧ�����Կ���С�����ꡱ����һ��ѧϰ��Ʒ��������ÿ�۳�1�иDz�Ʒ����30Ԫ��δ�۳�����Ʒÿ�п���10Ԫ������ͳ�����ϣ��õ�����Ʒ������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ������ͬѧΪ�˹���180�иò�Ʒ����x����λ���У�100��x��200����ʾһ�����ڵ��г���������y����λ��Ԫ����ʾһ�����ھ����ò�Ʒ������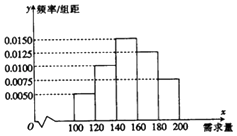
��1������ֱ��ͼ������������г�������x��ƽ������
��2����y��ʾΪx�ĺ�����
��3������ֱ��ͼ�����������������3800Ԫ�ĸ��ʣ���Ƶ�ʽ��Ƹ��ʣ���
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ�ã�
��������[100��120���ڵ�Ƶ��Ϊ��0.005��20=0.1��
��������[120��140���ڵ�Ƶ��Ϊ��0.01��20=0.2��
��������[140��160���ڵ�Ƶ��Ϊ��0.015��20=0.3��
��������[160��180���ڵ�Ƶ��Ϊ��0.0125��20=0.25��
��������[180��200]�ڵ�Ƶ��Ϊ��0.0075��20=0.15��
�����ֱ��ͼ������������г�������x��ƽ������
![]() =110��0.1+130��0.2+150��0.3+170��0.25+190��0.15=153��
=110��0.1+130��0.2+150��0.3+170��0.25+190��0.15=153��
��2���⣺��ÿ�۳�1�иDz�Ʒ����30Ԫ��δ�۳�����Ʒÿ�п���10Ԫ��
�൱100��x��180ʱ��y=30x��10��180��x��=40x��1800��
��180��x��200ʱ��y=30��180=5400��
��y= ![]()
��3���⣺����������3800Ԫ��
��40x��1800��3800����x��140��
���ɣ�1��֪��������3800Ԫ�ĸ���Ϊ��
1��0.1��0.2=0.7��
��������1����Ƶ�ʷֲ�ֱ��ͼ����������ָ����Χ�ڵ�Ƶ��ֵ�ٸ���ֱ��ͼ������������г�������x��ƽ������
2����������ɵú�������ʽ��100��x��180��һ�κ�������180<x��2 00�dz�������
3��������ɵ���������3800Ԫ���õ�x��140���������֪֪��������3800Ԫ�ĸ���Ϊ��1��0.1��0.2=0.7��
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ�ǽ����ĸ�������Ҫ֪��Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


