题目内容
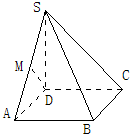
设一个正三棱锥的侧面与底面所成的角为α，相邻两个侧面所成的角为β，那么两个角α和β的三角函数间的关系是（ ）
| A．2cos2α+3cosβ=1 | B．2cosα+3cos2β=1 |
| C．3cos2α+2cosβ=1 | D．3cosα+2cos2β=1 |
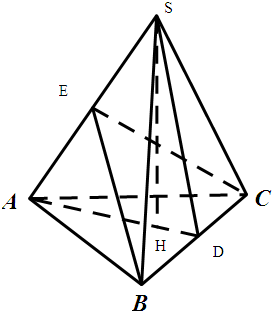
设正三棱锥S-ABC，侧面与底面所成的角为α，相邻两个侧面所成的角为β，作SD⊥BC，连接AD，作SH⊥AD，则SH⊥底面ABC，可得BE⊥SA，连接CE，则CE⊥SA，∠BEC是二侧面成角的平面角，
设AB=BC=AC=1个单位，
AD=
，HD=
=
，AH=
，
=cosα，SD=
，SH=
，
SA=
=
=
，
又BE×SA×
=SD×AB×
=S△SAB，
∴BE=
=
=
在三角形EBC中根据余弦定理，
BC2=BE2+EC2-2×BE×EC×cosβ，
1=
+
-2×
×cosβ，
经整理得：3cos2α+2cosβ=1，
故选C
设AB=BC=AC=1个单位，
AD=
| ||
| 2 |
| ||
|
| ||
| 6 |
| ||
| 3 |
| SD |
| HD |
| ||
| 6cosα |
| ||
| 6 |
SA=
| SH2+AH2 |
|
| ||
| 6 |
又BE×SA×
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
| SD×AB |
| SA |
| ||||
|
| 1 | ||
|
在三角形EBC中根据余弦定理，
BC2=BE2+EC2-2×BE×EC×cosβ，
1=
| 1 |
| 1+3cos2α |
| 1 |
| 1+3cos2α |
| 1 |
| 1+3cos2α |
经整理得：3cos2α+2cosβ=1，
故选C
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
