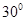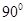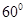题目内容
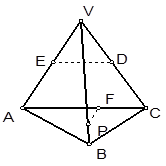
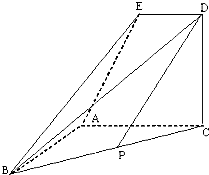
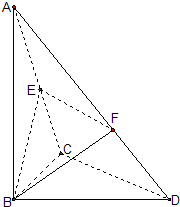
如图,已知ACDE是直角梯形,且ED∥AC,平面ACDE⊥平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2,ED=
AB,P是BC的中点.
(Ⅰ)求证:DP∥平面EAB;
(Ⅱ)求平面EBD与平面ABC所成锐二面角大小的余弦值.
| 1 |
| 2 |
(Ⅰ)求证:DP∥平面EAB;
(Ⅱ)求平面EBD与平面ABC所成锐二面角大小的余弦值.

(I)证明:取AB的中点F,连接PF,EF.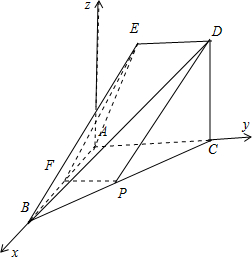
又∵P是BC的中点,∴FP
AC.
∵ED=
AB=
AC,ED∥AC,
∴FP
ED,
∴四边形EFPD是平行四边形,
∴PD∥EF.
而EF?平面EAB,PD?平面EAB,
∴PD∥平面EAB.
(II)∵∠BAC=90°,平面ACDE⊥平面ABC,∴BA⊥平面ACDE.
以点A为坐标原点,直线AB为x轴,AC为y轴,建立如图所示的空间直角坐标系,
则z轴在平面EACD内.则A(0,0,),B(2,0,0),E(0,1,
),D(0,2,
).
∴
=(2,-1,-
),
=(0,1,0).
设平面EBD的法向量
=(x,y,z),由
,得
,
取z=2,则x=
,y=0.∴
=(
,0,2).
可取
=(0,0,1)作为平面ABC的一个法向量,
∴cos<
,
>=
=
=
.
即平面EBD与平面ABC所成锐二面角大小的余弦值为
.

又∵P是BC的中点,∴FP
| ∥ |
| . |
| 1 |
| 2 |
∵ED=
| 1 |
| 2 |
| 1 |
| 2 |
∴FP
| ∥ |
| . |
∴四边形EFPD是平行四边形,
∴PD∥EF.
而EF?平面EAB,PD?平面EAB,
∴PD∥平面EAB.
(II)∵∠BAC=90°,平面ACDE⊥平面ABC,∴BA⊥平面ACDE.
以点A为坐标原点,直线AB为x轴,AC为y轴,建立如图所示的空间直角坐标系,
则z轴在平面EACD内.则A(0,0,),B(2,0,0),E(0,1,
| 3 |
| 3 |
∴
| EB |
| 3 |
| ED |
设平面EBD的法向量
| n |
|
|
取z=2,则x=
| 3 |
| n |
| 3 |
可取
| m |
∴cos<
| m |
| n |
| ||||
|
|
| 2 | ||
|
2
| ||
| 7 |
即平面EBD与平面ABC所成锐二面角大小的余弦值为
2
| ||
| 7 |

练习册系列答案
相关题目
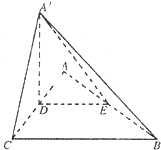
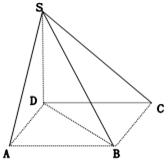

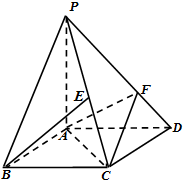
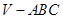 中,
中,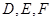 分别是
分别是 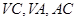 的中点,
的中点,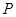 为
为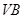 上任意一点,则直线
上任意一点,则直线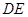 与
与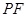 所成的角的大小是 ( )
所成的角的大小是 ( )