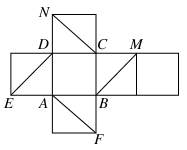
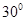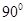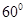题目内容
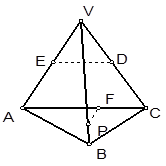
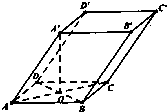
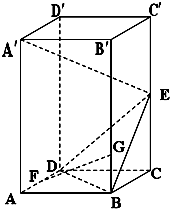
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
.
(1)证明:平面A′BD∥平面B′CD′;
(2)求二面角A-BC-B′的余弦值.
| 2 |
(1)证明:平面A′BD∥平面B′CD′;
(2)求二面角A-BC-B′的余弦值.

(1)证明:在四棱柱中,
∵BC∥A′D′,且BC=A′D′,
∴A′BCD′是平行四边形,
∴A′B∥CD′,
又∵A′B不包含于平面B′CD′,CD′?B′CD′,
∴A′B∥面B′CD′,
又A′B?面A′BD,A′D?面A′BD,且A′B∩A′D=A′,
∴平面A′BD∥平面B′CD′.
(2)∵平面ADD′A′∥平面BCC′B′,
∴二面角A-BC-B′与二面角A′-AD-B互补,
∵A′Q=1,AB=AA′=A′D=
,
∴A′Q2+OA2=AA'2,A′O2+OB2=A′B2,
∴A′O⊥OA,A′O⊥OB,
∴A′O⊥平面ABCD,
∴过O作OM⊥AD于M,连结A′M,
∴A′M⊥AD,∠A′MO为A′-AD-B的平面角,
cos∠A′MO=
=
,
∴二面角A-BC-B′的余弦值为-
.
∵BC∥A′D′,且BC=A′D′,
∴A′BCD′是平行四边形,
∴A′B∥CD′,
又∵A′B不包含于平面B′CD′,CD′?B′CD′,
∴A′B∥面B′CD′,
又A′B?面A′BD,A′D?面A′BD,且A′B∩A′D=A′,
∴平面A′BD∥平面B′CD′.
(2)∵平面ADD′A′∥平面BCC′B′,
∴二面角A-BC-B′与二面角A′-AD-B互补,
∵A′Q=1,AB=AA′=A′D=
| 2 |
∴A′Q2+OA2=AA'2,A′O2+OB2=A′B2,
∴A′O⊥OA,A′O⊥OB,
∴A′O⊥平面ABCD,
∴过O作OM⊥AD于M,连结A′M,
∴A′M⊥AD,∠A′MO为A′-AD-B的平面角,
cos∠A′MO=
| OM |
| A′M |
| ||
| 3 |
∴二面角A-BC-B′的余弦值为-
| ||
| 3 |

练习册系列答案
相关题目
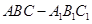 中,
中,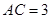 ,
,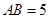 ,
,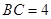 ,
,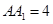 ,点
,点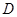 是
是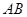 的中点.
的中点.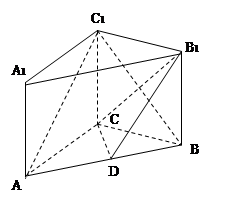
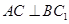 ;
; 
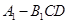 的体积.
的体积.
 中,
中,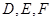 分别是
分别是 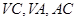 的中点,
的中点,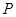 为
为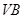 上任意一点,则直线
上任意一点,则直线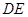 与
与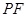 所成的角的大小是 ( )
所成的角的大小是 ( )